Изучение сложения гармонических колебаний одинаковой частоты

ЛАБОРАТОРНАЯ РАБОТА № 77

ИЗУЧЕНИЕ СЛОЖЕНИЯ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ ОДИНАКОВОЙ ЧАСТОТЫ

Цель работы: Изучить методы изменения разности фаз с помощью осциллографа. Измерить амплитуду и фазу результирующего колебания при сложении одинаково направленных колебаний в зависимости от их амплитуд и фаз. Изучить фигуры Лиссажу, получающиеся в результате сложения перпендикулярных колебаний.

1. КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ

Гармонические колебания описываются уравнением вида

s = Acos(wt + j₀),                                       (1)

где  s – смещение (величина, описывающая отклонение колебательной системы от положения равновесия); А – амплитуда колебаний (максимальное значение смещения); j = wt + j₀ – фаза колебаний; w – круговая частота; t – время; j₀ – начальная фаза (фаза в момент времени  t = 0).

Колебательная система одновременно может участвовать в нескольких колебательных процессах. Для определения зависимости смещения от времени в этом случае необходимо сложить гармонические колебания. В случае, когда колебания имеют одинаковую частоту и одно и то же направление, удобно воспользоваться методом векторных диаграмм (представления колебания с помощью вращающегося вектора). Этот метод состоит в том, что для колебания, задаваемого уравнением (1), из произвольной точки  О, выбранной на оси  s, под углом  j₀, равным начальной фазе колебания, откладывается вектор , модуль которого равен амплитуде (рис. 1).

Если теперь этот вектор привести во вращение с угловой скоростью  w  против часовой стрелки, то проекция конца вектора на ось  s  будет изменяться со временем по закону (1). Таким образом гармонические колебания можно представить проекцией на некоторую произвольно выбранную ось вектора амплитуды , отложенного из произвольной точки оси под углом , равным начальной фазе, и вращающегося с угловой скоростью вокруг этой точки против часовой стрелки.

Для того, чтобы применить этот метод к сложению гармонических колебаний 

s = s₁ + s₂ = A₁cos(wt + j₀₁) + A₂cos(wt + j₀₂)

построим их векторные диаграммы. Так как векторы  и  вращаются с одинаковой угловой скоростью  w, то разность фаз (j₂ – j₁) между ними остается постоянной.

Очевидно, что уравнение результирующего колебания будет

s = Acos(wt + j0), где амплитуда  А  равна длине вектора  ( =  + ), а начальная фаза  j₀  равна углу между ним и осью  s. Из рис. 2 по теореме косинусов и определению тангенса угла

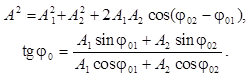  (2)

Эти соотношения останутся справедливыми и в том случае, если вместо начальных фаз взять фазы колебаний в любой (не обязательно начальный) момент времени  t. Если выбрать его так, чтобы фаза первого колебания была равна нулю, то

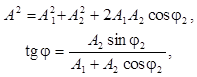                                         (3)

где  j₂ – разность фаз между вторым и первым колебаниями;  j – разность фаз между результирующим и начальным колебаниями.

Рассмотрим результат сложения двух гармонических колебаний одинаковой частоты  w, происходящих во взаимно перпендикулярных направлениях. В качестве начального выберем момент времени так, чтобы начальная фаза первого колебания была равна нулю:

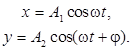                                                   (4)

Уравнение траектории результирующего колебания находится путем исключения из выражений (4) параметра  t:

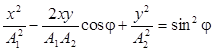.                                    (5)

Уравнение (5) есть уравнение эллипса. В общем случае ориентация его осей и их размеры зависят от амплитуд складываемых колебаний и разности фаз  j. Особый интерес представляют следующие частные случаи:

1) j = 0  и  j = p. В данном случае эллипс выражается в отрезок прямой, 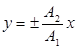 , где знак плюс соответствует случаю  j = 0, а знак минус —  j = p. Результирующее колебание является гармоническим колебанием с частотой  w  и амплитудой  .

2) j =    и  j =  . В данном случае уравнение (5) примет вид

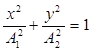.                                                    (6)

Это уравнение эллипса, оси которого совпадают с осями  х  и  y, а его полуоси соответственно равны амплитудам. Кроме того, если  А₁ = А₂, то эллипс (6) выражается в окружность.

Возвращаясь к общему случаю положим в уравнении (5)  х = 0. Значения  у*  при этом удовлетворяют уравнению 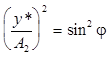 . Отсюда получим соотношение для определения фазы (рис. 3)

.                      (7)

Для электрических колебаний вместо амплитуд удобно воспользоваться действующими значениями напряжения (U₁  и  U₂), которые пропорциональны амплитудам, поэтому полученные для них формулы остаются справедливыми. Так при сложении одинаково направленных колебаний (при последовательном включении в электрическую цепь двух источников гармонического напряжения) получаем из (3)

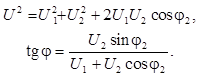                                          (8)

При сложении взаимно перпендикулярных колебаний, что осуществляется при подаче одного колебания на горизонтальную развертку осциллографа (вход  Х), а другого на вертикальную развертку (вход  У), на экране осциллографа электронный луч будет описывать эллипс, соответствующий уравнению (5) (при условии равенства коэффициентов усиления соответствующих каналов). При этом уравнение (7) позволяет (хотя и не очень точно) определить фазу по экрану (см. рис. 3). При этом следует иметь ввиду два обстоятельства. По уравнению (7) нельзя различить случаи фаз  j  и  p – j  (или что то же самое  j  и  –j). Поэтому конкретное значение  j  можно определить только с помощью дополнительных соображений (например, учитывая предыдущее значение фазы при ее изменении). Для корректного определения фазы необходимо, чтобы центр эллипса располагался в центре экрана. Для проверки этого обстоятельства можно воспользоваться координатной сеткой, нанесенной на экране.