Изучение сложения гармонических колебаний одинаковой частоты, страница 4

Используем метод комплексных амплитуд. При этом смещение (для электрических колебаний чаще всего напряжение) задается комплексным числом  , где  U₀ –амплитуда, а  j(t) = wt + j₀ – фаза колебаний в момент времени  t. Для электрических колебаний в линейных схемах (когда колебания остаются гармоническими с постоянной частотой  w). Практически важная задача состоит в определении разности фаз между колебаниями в разных точках схемы. При этом не описывают зависимость фазы от времени, следя только за ее постоянной составляющей. Тогда

,                                                      (11)

где   – так называемая, комплексная амплитуда напряжения. Здесь мы для простоты не указываем индекс "0" у фазы. Удобство этого метода состоит в том, различные элементы схемы характеризуются комплексными сопротивлениями. Так, например, для активного сопротивления  R:  , а для емкости  C:  . Сопротивление составных элементов рассчитываются по обычным формулам последовательного или параллельного соединения, а для определения комплексной силы тока используются законы Ома или правила Кирхгофа. Окончательно таким способом определяются амплитуды и фазы силы тока и напряжений для любых элементов электрической схемы.

Вернемся к схеме на рис. 7. Положим фазу входного напряжения(U_вх), которое по фазе совпадает с первым источником на схеме рис. 6, равной нулю. Тогда    будет действительной величиной. Обозначим ее  U₀. Сопротивление последовательно соединенных резистора  R₃  и емкости  C₁  равно

.

Для комплексной амплитуды силы тока, проходящего через  R₃  и  C₁  по закону Ома имеем

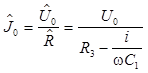, а для комплексной амплитуды напряжения в т.  D (относительно т. А)

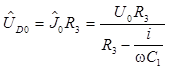.                                   (12)

Напряжение в т. В (относительно т. А) равно

.

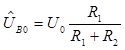Если как в схеме на рис. 6  R₁ = R₂, то

.                                                (13)

Напряжение на входе (U₂) имеет комплексную амплитуду , или с учетом (12) и (13)

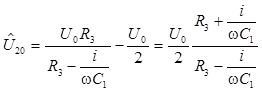.                             (14)

Второй множитель выражения (14) представляет собой отношение комплексно сопряженных чисел. Поэтому его модуль равен единице, а значит амплитуда выходного напряжения (U₂₀) не зависит от сопротивления  R₃. Для определения фазы выходного напряжения проведем преобразования:

.

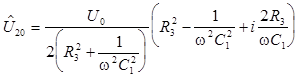Фазу определим через отношение мнимых и действительных частей комплексного числа:

.

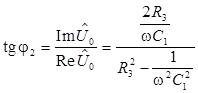После преобразований окончательно имеем

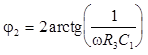.                                        (15)

По формуле (15) фаза меняется от  p (при  R₃ = 0) до  0 (при  R₃ ®¥). При условии  wR₃C₁ = 1  фаза  j₂ = .

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Запишите уравнение гармонических колебаний и дайте определения их основных характеристик.

2. В чем состоит метод векторных диаграмм, как он применяется в случае сложения двух одинаково направленных колебаний одинаковой частоты? Дайте вывод соотношения (2).

3. Рассмотрите случай сложения двух взаимно перпендикулярных колебаний одинаковой частоты и выведите формулу (5). Как можно наблюдать такое сложение?

4. Какой вид имеет фигура Лиссажу для случая сложения двух взаимно перпендикулярных колебаний одинаковой частоты и как она зависит от разности фаз между колебаниями? Указать частные случаи, представляющие собой интерес.

5. Как измерить разность фаз по виду фигуры Лиссажу на экране ЭО? Выведите формулу (7).

6. Как измерить разность фаз по сдвигу синусоиды на экране ЭО? Как для этого следует подключить осциллограф? Выведите формулу (9).

7*. Приведите электрическую схему фазовращателя и укажите назначение его основных элементов.

8*. В чем состоит метод комплексных амплитуд и для каких случаев его можно применять?

9*. Примените метод комплексных амплитуд для расчета работы фазовращателя. Выведите формулу (14).

10*. Как определить изменение фазы выходного напряжения фазовращателя по отношению к входному напряжению? Выведите формулу (15).