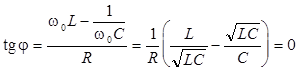Исследование вынужденных колебаний в электрическом контуре, страница 2

.

Совпадение по фазе силы тока и внешнего напряжения при резонансе в данной работе используется как удобный критерий для контроля его достижения.

Прежде чем исследовать резонансные кривые (зависимости U_m и J_m от  w  в окрестности w_р) введем еще один параметр, который наряду с резонансной частотой характеризует явление резонанса в контуре — его добротность  Q. Он определяется как отношение энергии, запасенной в контуре во время вынужденных установившихся колебаний при резонансе, к средней потере энергии на активном сопротивлении (например, в виде джоулева тепла) за время, в течение которого фаза колебаний меняется на один радиан. Потери энергии на сопротивлении  R  за период  Т

.

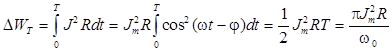За время изменения фазы на один радиан средняя потеря энергии в  2p  раз меньше

.

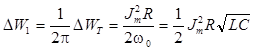Для установившихся колебаний полная запасенная в контуре энергия постоянна и ее проще всего рассчитать в том момент, когда сила тока максимальна, а напряжение на конденсаторе равно нулю, как энергию магнитного поля в катушке

.

С учетом двух последних соотношений из определения добротности для контура следует

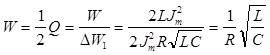.                         (12)

Резонансные кривые удобно исследовать, предварительно определив максимальные значения амплитуд напряжения и силы тока  U_m,р и J_m,р. Из (10а) и (11) можно получить, что при  w » w₀

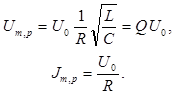                                      (13)

Из соотношений (13) видно, что необходимым условием резкого возрастания амплитуд при  w ® w₀  является слабое затухание, т.к. условия  b << w₀  и  Q >> 1  эквивалентны (в общем случае ).

На практике при резонансе  U_m,p >> U₀, (напряжение на конденсаторе во много раз превышает напряжение внешнего источника), что с одной стороны создает опасность пробоя конденсаторов, разрушения изоляции проводов и т. п., а с другой стороны используется для селективного усиления сигналов необходимой частоты, например, при настройке радиоприемника на определенную частоту и т. п.

Соотношение (13) дает один из практических способов определения добротности контура

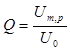,                                            (13а)

т. е. ее можно определить как отношение амплитуды напряжения на конденсаторе при резонансе к амплитуде при нулевой частоте (см. 8а).

Другой способ состоит в определении "остроты" резонансных кривых. В малой окрестности  w₀ ( при условии |w – w₀| << w₀) зависимости  U_m  и  J_m  от  w (10а) и (11) имеют один и тот же функциональный вид

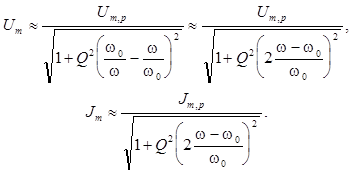                (14)

Форму резонансной кривой чаще всего характеризуют шириной  2Dw (Dw = |w – w₀|), измеренной на уровне 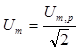(или 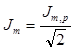). Из (14) следует, что при таком условии (рис. 4)

.                                             (15)

Используемая в данной работе установка имеет ряд особенностей, учет которых несколько меняет вид расчетных формул и необходим для правильной интерпретации полученных результатов. Во-первых, используемые в установке вольтметры измеряют не амплитудные значения напряжений, а действующие значения, которые пропорциональны амплитудным. Т. к. соотношения (10), (11), (13) и (13а) однородны относительно токов и напряжений, то для учета вышесказанного будем считать, что в них и в дальнейшем используются соответствующие действующие значения. Во-вторых, вместо силы тока в работе измеряется падение напряжения на специальном резисторе  R*  небольшого сопротивления (U_R = R*J_m). Очевидно, что форма резонансной кривой при этом не изменится. В-третьих, используемый в установке звуковой генератор проградуирован не в единицах круговой частоты  w (рад/с), а в единицах частоты  n (Гц). В связи с этим вместо многократного пересчета частот можно рекомендовать в работе вместо соотношения (5) использовать выражение