


27. Понятие кусочно-гладкой пространственной кривой. Определение криволинейного интеграла по длине дуги(=1-го рода) и его вычисление.
![]() Пространственная кривая Г называется кусочно-гладкой,
если её можно задать параметрически, т.е. в виде (1).
Пространственная кривая Г называется кусочно-гладкой,
если её можно задать параметрически, т.е. в виде (1).
Функции φ(t), ψ(t), χ(t)
непрерывны на отрезке [α, β] и этот отрезок можно разбить на конечное число
частей, внутри каждой из которых функции φ(t), ψ(t), χ(t)
непрерывно дифференцируемы (имеют непрерывные производные) не равные нулю
одновременно. Кривая (1) называется замкнутой, если φ(α)=φ(β), ψ(α)=ψ(β), χ(α)=χ(β). Кривая Г, не имеющая точек самопересечения
называется простой кривой. Пусть в пространстве Oxyz задан контур ![]() и на нем определены три ограниченные
функции P(x,y,z), Q(x,y,z) и R(x,y,z). Разобьем контур на n частей
произвольно точками
и на нем определены три ограниченные
функции P(x,y,z), Q(x,y,z) и R(x,y,z). Разобьем контур на n частей
произвольно точками ![]() двигаясь от А к В. Получим n дуг
двигаясь от А к В. Получим n дуг ![]() . Произвольное разбиение обозначим через τ. На
каждой дуге возьмем точку (произвольно)
. Произвольное разбиение обозначим через τ. На
каждой дуге возьмем точку (произвольно) ![]() . Они
называются промежуточными точками разбиения τ. Пусть
. Они
называются промежуточными точками разбиения τ. Пусть ![]() , а
, а ![]() .
Положим Δxk=xk-xk-1;Δyk=yk-yk-1;Δzk=zk-zk-1; ΔSk=|Mk-1Mk|, k=1,2…n;
.
Положим Δxk=xk-xk-1;Δyk=yk-yk-1;Δzk=zk-zk-1; ΔSk=|Mk-1Mk|, k=1,2…n; ![]() ;
;![]()
λτ - ранг разбиения τ.
Повторим выкладку, приведшую к построению криволинейного интеграла второго рода.
![]() ;
; ![]() ,
, ![]() .
.
Заменив Δxk на ΔSk получим криволинейный интеграл по длине дуги или криволинейный интеграл первого рода.
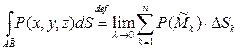 ,
, ![]() ,
, ![]() .
.
Причём ориентация дуги уже не важна.
Св–ва 1. Если ф–ция P(x,y,z)
кусочнонепрерывна на дуге ![]() , то интеграл
существует. 2.
, то интеграл
существует. 2. ![]() .3. Справедлива теорема о среднем
значении: Если ф–ция P(x,y,z) непрерывна на дуге
.3. Справедлива теорема о среднем
значении: Если ф–ция P(x,y,z) непрерывна на дуге ![]() , то
существует точка М0(x0,y0,z0) такая,
что
, то
существует точка М0(x0,y0,z0) такая,
что ![]() и
и ![]()
Если вдоль дуги ![]() непрерывным
образом распределена масса с плотностью γ (x,y,z) в
точке М(x,y,z), то значение всей массы m распределённой
вдоль дуги
непрерывным
образом распределена масса с плотностью γ (x,y,z) в
точке М(x,y,z), то значение всей массы m распределённой
вдоль дуги ![]()
![]() .
.
Криволинейные интегралы первого рода вычисляются путем преобразования их в определённые интегралы.
Пусть ![]() задана параметрически
задана параметрически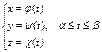 . Пусть на дуге задана непрерывная функция f(x,y,z).
. Пусть на дуге задана непрерывная функция f(x,y,z).
По аналогии с двумерным случаем ![]() .
Поэтому
.
Поэтому ![]() .
.
28. Понятие ориентированной кусочно-гладкой пространственной кривой. Опр–ние криволинейного интеграла по координатам, механический смысл и основные св–ва.
Кривая Г называется ориентированной или контуром, если
зафиксировано одно из двух ее возможных направлений. Если контур Г является не
замкнутым, то он имеет начало А и конец В. В этом случае пишут ![]() . Если контур Г замкнутый, за конец и
начало можно взять любую точку контура.
. Если контур Г замкнутый, за конец и
начало можно взять любую точку контура.
Пусть в пространстве Oxyz задан контур ![]() и на нем определены три ограниченные
функции P(x,y,z), Q(x,y,z) и R(x,y,z). Разобьем контур на n частей
произвольно точками
и на нем определены три ограниченные
функции P(x,y,z), Q(x,y,z) и R(x,y,z). Разобьем контур на n частей
произвольно точками ![]() двигаясь от А к В. Получим n дуг
двигаясь от А к В. Получим n дуг ![]() . Произвольное разбиение обозначим через τ. На
каждой дуге возьмем точку (произвольно)
. Произвольное разбиение обозначим через τ. На
каждой дуге возьмем точку (произвольно) ![]() . Они
называются промежуточными точками разбиения τ. Пусть
. Они
называются промежуточными точками разбиения τ. Пусть ![]() , а
, а ![]() .
Положим Δxk=xk-xk-1;Δyk=yk-yk-1;Δzk=zk-zk-1; ΔSk=|Mk-1Mk|, k=1,2…n;
.
Положим Δxk=xk-xk-1;Δyk=yk-yk-1;Δzk=zk-zk-1; ΔSk=|Mk-1Mk|, k=1,2…n; ![]() ;
;![]()
λτ - ранг разбиения τ.
Суммы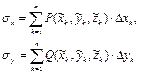
![]() называются интегральными суммами функций P, Q и R
соответственно отвечающими заданному разбиению τ контура
называются интегральными суммами функций P, Q и R
соответственно отвечающими заданному разбиению τ контура ![]() на части и заданному выбору промежуточных
точек
на части и заданному выбору промежуточных
точек ![]() на указанных частях.
на указанных частях.
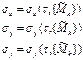
Опр: Число I
называется конечным пределом интегральных сумм σx (σy,σz) при λ→0 и пишут ![]() если для любого ε>0
существует д>0 такое, что для любого разбиения τ контура на части
с условием λ<д и любого выбора промежуточных точек
если для любого ε>0
существует д>0 такое, что для любого разбиения τ контура на части
с условием λ<д и любого выбора промежуточных точек ![]() будет выполняться неравенство
будет выполняться неравенство ![]() .
.
Опр: Если
существует конечный предел ![]() , то он называется
криволинейным интегралом от функции P(x,y,z) [Q(x,y,z), R(x,y,z)] по
координате х (у, z) вдоль контура
, то он называется
криволинейным интегралом от функции P(x,y,z) [Q(x,y,z), R(x,y,z)] по
координате х (у, z) вдоль контура ![]() и
обозначается символом
и
обозначается символом
![]()
Их наз. криволинейными интегралами по коорд. первого рода.
Сумму этих интегралов обозначают ![]() и называют общим криволинейным интегралом
или криволинейным интегралом второго рода общего вида.
и называют общим криволинейным интегралом
или криволинейным интегралом второго рода общего вида.
Выясним механический смысл криволинейного интеграла второго рода.
Пусть вдоль контура ![]() движется
материальная точка под действием переменной силы
движется
материальная точка под действием переменной силы ![]() .
Найдём работу W производимую силой при перемещении точки из положения
А в положение В (Р(М), Q(М) и R(М) непрерывны).
.
Найдём работу W производимую силой при перемещении точки из положения
А в положение В (Р(М), Q(М) и R(М) непрерывны).
![]()
![]() .Переходя
к пределу, получаем:
.Переходя
к пределу, получаем: ![]()
Основные св–ва: 1. Криволинейные интегралы второго рода
от кусочно-непрерывных функций вдоль кусочно-гладких контуров существуют. 2. Если
направление контура интегрирования изменить на противоположное, то
криволинейный интеграл сменит знак. 3. Свойство аддитивности. 4. Криволинейный
интеграл по замкнутому контуру не зависит от выбора начальной точки, а зависит
от направления обхода. 5. Пусть квадрируемая область D, ограниченная
замкнутым контуром Г, разбита на две части D1 и D2 некоторой
дугой γ. Тогда криволинейный интеграл по контуру Г будет равен сумме интегралов
по контурам Г1 и Г2, ограничивающим области D1, D2 и
проходимом в том же направлении, что и γ. ![]() .
.
6. Св–во линейности. 7. Интеграл по координате х [y,z] вдоль контура, лежащего в плоскости перпендикулярной оси Ох [Oy, Oz] равен нулю.
29. Вычисление криволинейных интегралов по координатам.
Пусть требуется вычислить интеграл ![]() , где P, Q и R -
функции кусочно-непрерывные на контуре
, где P, Q и R -
функции кусочно-непрерывные на контуре ![]() . Пусть
. Пусть
![]() :
: 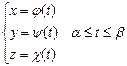 , где функции φ(t), ψ(t), χ(t)
непрерывны на отрезке [α, β] и имеют непрерывные производные. Пусть tA=α, tB=β, либо tB=α, tA=β, в зависимости от направления интегрирования.
, где функции φ(t), ψ(t), χ(t)
непрерывны на отрезке [α, β] и имеют непрерывные производные. Пусть tA=α, tB=β, либо tB=α, tA=β, в зависимости от направления интегрирования.
![]() , где
, где ![]() , а
, а ![]() , а
, а ![]() может быть взята на дуге
может быть взята на дуге ![]() совершенно произвольно. Пусть tk - значение параметра t, отвечающее точке Mk с
координатами Mk(xk,yk,zk). Имеем
совершенно произвольно. Пусть tk - значение параметра t, отвечающее точке Mk с
координатами Mk(xk,yk,zk). Имеем ![]() .
.
Будем считать, что точка ![]() выбрана
так, что ее абсцисса
выбрана
так, что ее абсцисса ![]() , ордината
, ордината ![]() , а
, а ![]() , то
есть выбрана так, что ей соответствует значение
, то
есть выбрана так, что ей соответствует значение ![]() параметра
t и это при k=1,2…,n. Тогда (2) можно переписать в виде
параметра
t и это при k=1,2…,n. Тогда (2) можно переписать в виде
![]()
Справа в (3) стоит предел интегральной суммы для
обычного определённого интеграла от функции F(t)=P(φ(t),ψ(t),χ(t)).φ’(t), для промежутка с концами tA и tB. Тогда (3) запишется в виде
![]() (4)
(4)
Аналогично![]() и
и ![]() . Окончательно:
. Окончательно:
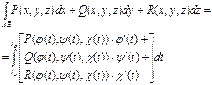
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.