Понятие кусочно-гладкой пространственной кривой. Определение криволинейного интеграла по длине дуги (=1-го рода) и его вычисление. Понятие ориентированной кусочно-гладкой пространственной кривой. Определение криволинейного интеграла по координатам, механический смысл и основные свойства. Вычисление криволинейных интегралов по координатам, страница 4

Пусть задана гладкая или кусочно-гладкая поверхность π. Выберем на этой поверхности определённую сторону, т.е. ориентируем поверхность. Пусть для определённости π задана уравнением z=φ(x,y), где φ(x,y) - функция непрерывная в области D, где D - проекция φ(x,y) на Oxy. Если выбрана верхняя сторона поверхности π, то углы нормали в точках поверхности π образуют с осью Oz острые углы (в точках границы π углы могут быть прямыми). Если выбрана нижняя сторона поверхности π, то углы нормалей с осью Oz будут тупыми (в точках границы поверхности углы могут быть прямыми). Пусть на поверхности π произвольно на n частей π₁,π₂,…,π_n. Полученное разбиение обозначим через τ. Разбиение τ поверхности π на части π₁,π₂,…,π_n порождает соответствующее разбиение области D на части D₁,…,D_n, где . Пусть , где d_k - диаметр части  π_k. λ - ранг разбиения τ. На каждой части π_k выберем произвольно точку M_k. Тогда  {M_k} называются промежуточными точками разбиения τ.

Пусть ΔS_k  - площадь области D_k, а

Составим сумму  (1). Суммы такого вида называются интегральными суммами функции R(x,y,z), заданной поверхности π.

Опр: Число I называют конечным пределом интегральных сумм (1) при λ→0, если для любого ε>0 существует δ>0 такие, что при любом разбиении τ поверхности π на части с условием  λ< δ  и любом выборе промежуточных точек на этих частях будет выполниться |σ-I|<ε. При этом пишут .

Опр: Если конечный предел интегральных сумм (1) существует, то он называется поверхностным интегралом по выбранной стороне поверхности по координатам х и у или поверхностным интегралом второго рода и обозначается .

Аналогично определяются поверхностные интегралы второго рода по координатам z и х, у и z: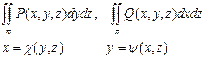

Сумма трех записанных интегралов называется общим поверхностным интегралом второго рода .

36.Вычисление поверхностных интегралов 2-го рода.

Вычисление интегралов второго рода следующим образом сводится к вычислению двойного интеграла.

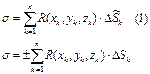
в таком виде σ является интегральной суммой двойного интеграла ±R(x,y,φ(x,y)), поэтому справедлива формула

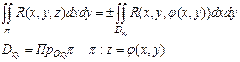
Аналогично выводятся формулы:

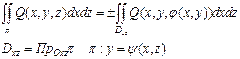
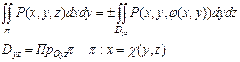
37.Связь между поверхностными интегралами 1-го и 2-го рода.

Пусть на π определены P(x,y,z), Q(x,y,z) и R(x,y,z). Пусть , ,  - направляющие косинусы единичной нормали, выбранной на стороне π.

Тогда справедливы формулы

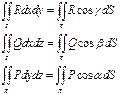
, где .

Величина  называется потоком вектора  через выбранную поверхность π.

П - количество жидкости, протекающей через π в направлении вектора  за единицу времени, если  - скорость идеальной жидкости в точке М.

В основе доказательства приведённых формул лежит обобщение следующей теоремы: Если π₁ и π₂ две плоскости, угол между которыми φ¹π/2 и Ф₁ и Ф₂ геометрические фигуры в плоскостях π₁ и π₂ соответственно, , то .

Тогда .

38. Теорема Остроградского о связи поверхностного интеграла 2-го рода с соответствующим тройным интегралом.

Пусть Т - замкнутая пространственная область ограниченная гладкой или кусочно-гладкой поверхностью π. А функции Р(х,у,z), Q(x,y,z) и R(x,y,z) непрерывны на π вместе с частными производными первого порядка , тогда  (1)

Интеграл (1) в правой части (1) берётся по внешней стороне поверхности. (1) - формула Остроградского.

(2) величина  называется дивергенцией вектора  и обозначается .

Используя понятие дивергенции и потока (1) можно записать  (1')

39. Теорема Стока о связи криволинейного интеграла по координатам с соответствующим поверхностным интегралом 2-го рода. Ротор и циркуляция векторного поля, теорема Стокса в векторной форме.

π - гладкая или кусочно-гладкая незамкнутая в геометрическом смысле ориентированная поверхность, ограниченная гладким или кусочно-гладким контуром Г. Пусть на π определены функции Р, Q и R, непрерывные вместе с частными производными первого порядка , тогда справедлива следующая формула , где интегрирование ведётся по выбранной стороне π и положительному направлению Г.

Замечание: Если поверхность π - область плоскости Оху, то dzdx=0 и dydz=0 и формула Стокса переходит в формулу Грина.

Вектор  называется ротором (или вихрем) вектора  и обозначается . Характеризует в каждой точке вращательные способности поля.

.

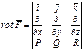Замечание: Формула Стокса в векторной форме имеет вид: , где .

Опр:  называется циркуляцией поля вектора . Она характеризует вращательную способность поля вдоль контура Г.