Дополнительные сведения о системе MathCAD.
Система MathCAD содержит встроенный датчик равновероятных псевдослучайных чисел "rnd(A)", где A - число, определяющее диапазон ненулевой вероятности. Например, если определить
n:=1.. 100 sn := rnd(1)
то результатом будет последовательность из ста независимых псевдослучайных чисел, имеющих равномерное распределение в интервале (0,1). При повторном запуске этого же документа будет воспроизведена та же последовательность. Если нужно получить другую реализацию с тем же распределением, можно использовать пункт меню Math Options, задавая параметр "seed" (по умолчанию равный 1). Присваивая этой величине разные значения, можно порождать различные реализации случайных последовательностей.
В радиотехнических задачах чаще требуется генерировать случайные величины с нормальным (гауссовым) распределением. Равновероятные на (0,1) случайные числа могут быть преобразованы в гауссовские случайные числа с нулевым математическим ожиданием и единичной дисперсией при помощи следующего преобразования
![]()
где sn и qn- различные некоррелированные случайные последовательности с равномерным на (0,1) распределением. При помощи преобразования
![]()
получается
другая последовательность гауссовских некоррелированных случайных величин,
причем ![]() и
и ![]() некоррелированны между собой.
некоррелированны между собой.
(Заметим, что в системе MathCAD имеется встроенная функция rnorm, позволяющая генерировать целиком вектор, составленный из заданного количества независимых компонент с нормальным (гауссовским) распределением.)
Чтобы получить коррелированную случайную последовательность, можно использовать один из двух подходов. Первый подход основан на временной фильтрации некоррелированной последовательности при помощи разностного уравнения рекурсивного или нерекурсивного фильтра. Второй подход заключается в умножении спектра (БПФ) последовательности на коэффициент передачи фильтра (фильтрация в частотной области).
Применение БПФ в системе MathCAD имеет ряд особенностей.
Рассмотрим вначале прямое БПФ вещественной последовательности, которому соответствует встроенная функция "fft()".
Аргументом функции "fft()" должен быть массив длины 2m,где m - целое положительное число. Результат выполнения этой функции - тоже массив, но его длина составляет всего 1+2m-1; симметрия спектра вещественной последовательности позволяет экономить память при хранении спектральных отсчетов. Поэтому аргументом функции обратного БПФ "ifft()" должна быть последовательность (массив) длины 1+2m-1; результатом выполнения этой функции будет массив длины 2m. Пример применения БПФ:
U = fft (V); V = ifft (U), где V - последовательность длины 64, а U - последовательность длины 33.
Для преобразований комплексных последовательностей в системе MathCAD имеется вторая пара встроенных функций "cfft()" и "icfft()"; аргументами обеих функций должны быть массивы длины 2m, например
W = cfft (V); V = icfft (W), где V и W - массивы комплексных чисел длины 128.
Чтобы сформировать узкополосную случайную последовательность, можно задать АЧХ формирующего фильтра, например, в виде
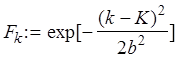 .
.
Сформированная случайная последовательность может быть сохранена на диске для использования в последующих работах. Для этого нужно использовать встроенную функцию "WRITEPRN":
WRITEPRN(filename) := r1n
В результате выполнения этой функции последовательность r1n будет записана на диск в файл с именемfilename. Для того, чтобы считать информацию с диска, используется встроенная функция "READPRN":
Sn:= READPRN(filename.DAT)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.