Нелинейные элементы и воздействие на них гармонических и полигармонических колебаний

Теория производит тем большее впечатление, чем проще ее предпосылки. С тех пор, как на теорию относительности навалились математики, я сам перестал ее понимать.

Альберт Эйнштейн

 глава 8

НЕЛИНЕЙНЫЕ ЭЛЕМЕНТЫ И ВОЗДЕЙСТВИЕ НА НИХ ГАРМОНИЧЕСКИХ И ПОЛИГАРМОНИЧЕСКИХ КОЛЕБАНИЙ

8.1.         Изучаемые вопросы

Общие сведения. Задачи и критерии аппроксимации. Аппроксимирующие функции. Определение коэффициентов аппроксимации [1, 8.1, 8.2; 2, 11.1].

Спектральный состав выходного колебания в нелинейном элементе при гармоническом воздействии (гармонический анализ). Методы анализа с использованием: классических формул, формул трех и пяти ординат, тригонометрических формул кратных аргументов, функций Бесселя, угла отсечки и функций Берга. Спектральный анализ при бигармоническом и полигармоническом воздействии. Комбинационные частоты [2, 11.2, 11.4; 1, 8.3, 8.4; 3, 6.2].

8.2.         Краткие теоретические сведения

    Аппроксимация характеристик нелинейных элементов

Характеристики нелинейных элементов (НЭ) в большинстве случаев задаются графически (из справочника) или таблично (в ходе эксперимента), поэтому при анализе и расчете схем с НЭ первостепенной стоит задача аппроксимации, т. е. приближенного аналитического представления характеристики НЭ.

Общая задача аппроксимации включает в себя две самостоятельные задачи:

·  выбор класса подходящей функции;

·  определение коэффициентов аппроксимации.

Выбор класса аппроксимирующей функции. Решая эту задачу, необходимо соблюдать требования, в значительной степени противоречивые: 1) простоту функции; 2) достаточную точность (ошибка аппроксимации должна быть одного порядка с разбросом параметров отдельных элементов в партии); 3) наглядность, позволяющую судить об изменении коэффициентов аппроксимации при изменении положения рабочей точки и т. п.; 4) ясность понимания процессов в схеме и выявления свойств схемы, представляющих интерес в конкретном случае. Например, для выявления и объяснения особенности работы автогенератора, надо аппроксимировать характеристику НЭ полиномом различной степени, вплоть до пятой. Поэтому часто приходится по-разному аппроксимировать одну и ту же характеристику в зависимости от режима работы НЭ, назначения схемы, исследуемых вопросов.

В теории радиотехнических цепей (и вообще в радиотехнике) для аппроксимации характеристик НЭ наиболее часто используют следующие функции.

1. Степенной полином:

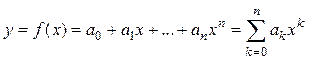.                    (8.1)

Для окрестности с рабочей точкой  полином (8.1) можно записать в виде ряда Тейлора

 =

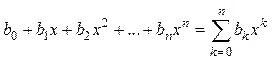= ,                     (8.2)

где

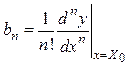.                                      (8.3)

Обычно , при этом в ряде случаев характеристика может содержать только четную или только нечетную часть.

Полиномом первой степени аппроксимируют линейные участки характеристик НЭ только при изучении линейных явлений. Параболу используют для аппроксимации начальных участков характеристик НЭ при действии малых входных сигналов. Укороченный полином третьей степени (без члена ) применяют в том случае, если надо передать замедление роста функции (усилительных свойств НЭ) с увеличением входного сигнала, при этом .

2. Экспоненциальный полином:

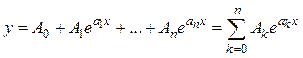.                     (8.4)

В ряде случаев используют лишь одну экспоненту. Например, характеристика вакуумного диода представляется выражением

,                                           ()

а полупроводникового диода

,                            ()

где , .

3. Степенная функция:

,                                             (8.5)

где  – дробное число.

4. Кусочно-линейная и кусочно-нелинейная функции. Реальная плавно изменяющаяся зависимость  заменяется приближенной, состоящей из отрезков прямых и кривых.

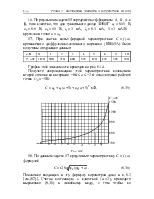
На рис. 8.1 в качестве примера приведены характеристики, аппроксимированные двумя отрезками: а) прямых линий; б) прямой и параболы.

Наиболее широкое использование получила кусочно-линейная аппроксимация. Она обеспечивает достаточную точность только при больших амплитудах воздействующих сигналов, а потому применяется при расчетах мощных усилителей, генераторов, умножителей частоты, некоторых схем модуляторов, детекторов и др.

5. Трансцендентные функции: гиперболические тангенс и синус, функция Гаусса, тригонометрические функции и др. В первую очередь следует отметить функцию, содержащую гиперболический тангенс

,                                     (8.6)

предложенную Н. И. Крыловым, которая хорошо описывает симметричные характеристики и изменения производной (крутизны) и второй производной (кривизны) ряда вольт-амперных характеристик (ВАХ) ламп и транзисторов.

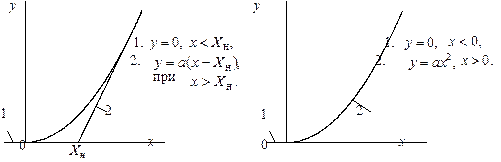
а                                                                         б

Рис. 8.1

Аппроксимация реактивных (индуктивных и емкостных) НЭ ничем не отличается от аппроксимации резистивных НЭ – ламп, транзисторов и др. Используются как упомянутые функции, так и другие. Например, вольт-фарадная характеристика p-n-перехода полупроводникового элемента аппроксимируется выражением:

,                               (8.7)

где  – напряжение (обратное) на переходе;  – высота потенциального барьера (контактная разность потенциалов);  – емкость перехода при отсутствии внешнего напряжения ();  – постоянная, зависящая от распределения примесей.