Нелинейные элементы и воздействие на них гармонических и полигармонических колебаний, страница 3

.

Подставив в полином входной сигнал , получим

.

Воспользовавшись известными формулами тригонометрических функций кратных аргументов (прил. П.1), получим:

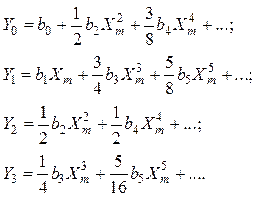                        (8.14)

3. Метод с использованием модифицированных функций Бесселя. Характеристика НЭ аппроксимируется экспонентой, и разложению в ряд Фурье должны быть подвергнуты выражения вида

   или   .

Экспоненты в этих выражениях разлагаются в ряды:

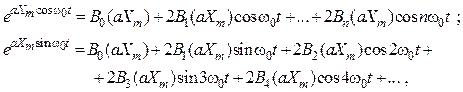   (8.15)

где  – модифицированная функция Бесселя -го порядка от аргумента . Таблица значений и графики этих функций приведены в прил. П.11.

Используя, например, первое из соотношений (8.15), получаем

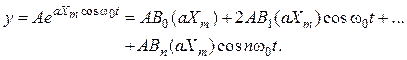
Из сопоставления этого выражения с формулой (8.10) следует

;    .                     (8.16)

4. Метод с использованием угла отсечки и функций Берга. Этот метод применим для аппроксимации характеристик НЭ кусочно-линейной зависимостью и разработан акад. А. И. Бергом. Сущность метода поясняется на рис. 8.4.

Основные расчетные соотношения:

;                               (8.17)

;                                (8.18)

,                             (8.19)

где  и  – функции Берга (коэффициенты гармоник), расчетные формулы, численные значения и графики для которых приведены в прил. П.9. Эти функции имеют максимальные значения  и  при соответствующем оптимальном угле

, ,                   (8.20)

Рис. 8.4

Если – vario, а , то максимум амплитуды -й гармоники на выходе НЭ рассчитывается с использованием значения

,                                  (8.21)

если же , а  и  варьируются, то

.                                  (8.22)

Совершенно аналогично вводится понятие верхнего угла отсечки  (см. кривые 2 на рис. 8.4) для тех случаев, когда необходимо учитывать характерный верхний изгиб (насыщение ) характеристики НЭ.

5. Метод с использованием функций Бесселя. Применяется в тех случаях, когда аппроксимирующее выражение содержит тригонометрические или гиперболические функции синуса и косинуса, которые разлагаются по бесселевым (цилиндрическим) функциям. Соответствующие формулы приведены в прил. П.10. Например, при аппроксимации вида

имеем

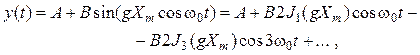
,                                   (8.23)

где  – функции Бесселя первого рода -го порядка. Таблица значений и графики нескольких функций приведены в прил. П.10.

   Спектральный анализ. Комбинационные составляющие

Это случай воздействия на НЭ сложного колебания, состоящего из двух и более синусоидальных колебаний. При этом на выходе НЭ будут иметь место как гармонические, так и комбинационные составляющие. Задача спектрального анализа состоит в определении амплитуд и фаз этих составляющих.

С точки зрения простоты спектрального анализа используют лишь два класса аппроксимирующих функций: степенной полином и экспоненту.

1. Степенной полином. В этом случае для нахождения спектра нужно пользоваться тригонометрическими формулами кратных аргументов и формулами произведений синусов и косинусов (см. прил. П.1).

Например, при подаче на вход НЭ бигармонического колебания с частотами  и  на выходе будет ряд составляющих

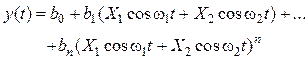
с частотами

,                                    (8.24)

где  и  – целые числа натурального ряда, включая нули. Если  или  равны нулю, то имеют место гармонические составляющие выходного сигнала, а если они не равны нулю, то – комбинационные, обозначаемые символом  (также с двойным индексом).

Пример спектра при воздействии трехкомпонентного входного сигнала на НЭ, характеристика которого аппроксимирована полиномом третьей степени, дан в прил. П.8.

Спектральный анализ при относительно большом числе составляющих входного сигнала и/или высокой степени аппроксимирующего полинома становится громоздким. Поэтому такой путь анализа непродуктивен и следует обращаться к аппроксимации экспонентой.