




















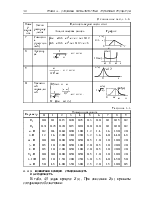

Объясню, как смогу: не буду говорить ничего окончательного и определенного, подобно оракулу Аполлона, а, будучи всего лишь слабым смертным, укажу только правдоподобные предположения.
Цицерон
 глава 4
глава 4
ОСНОВНЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ПРОЦЕССОВ
4.1. Изучаемые вопросы
Случайные колебания как сигнал и как помеха. Одномерный и многомерный законы распределения вероятностей. Характеристические и моментные функции. Стационарные и эргодические процессы; определение характеристик и параметров процесса усреднением по времени [3, гл.17; 2, 6.3; 1, 4.1, 4.2].
Корреляционное представление случайных процессов. Корреляционные функции и их свойства. Спектральное представление. Спектральная плотность мощности. Теорема Винера-Хинчина [3, 17.9 и 18; 1, 4.3…4.5; 2, 7.1, 7.2].
Узкополосные случайные процессы. Статистические характеристики огибающей и фазы [1, 4.6; 2, 7.3].
Указания. Следует обратить внимание на радиотехническую интерпретацию таких понятий, как математическое ожидание, средний квадрат, дисперсия, корреляционная функция и другие, на свойства спектрально-корреляционных характеристик случайного процесса. Основные характеристики полезно рассматривать на примерах наиболее часто встречающихся в природе и технике связи нормальных (гауссовых) процессов. При анализе радиоцепей весьма продуктивны модели процессов в виде белого шума и узкополосного сигнала.
Наиболее полно вопросы темы изложены в работах [10, 11]. Руководства и учебные пособия [8, 9, 5, 6] содержат большое число примеров задач с решениями, указаниями и комментариями.
4.2. Краткие теоретические сведения
Случайный процесс ![]() может быть
охарактеризован во временной области совокупностью (ансамблем) реализаций
может быть
охарактеризован во временной области совокупностью (ансамблем) реализаций ![]() , т. е.
, т. е.
![]() (4.1)
(4.1)
Если зафиксировать произвольный момент времени ![]() , т. е. получить сечение процесса – случайную
величину
, т. е. получить сечение процесса – случайную
величину ![]() , то эту величину (как следует из курса
теории вероятностей) можно статистически полностью охарактеризовать функцией распределения
, то эту величину (как следует из курса
теории вероятностей) можно статистически полностью охарактеризовать функцией распределения ![]() или
плотностью вероятности
или
плотностью вероятности ![]() . Обе функции
выражают одномерный закон распределения случайной величины
. Обе функции
выражают одномерный закон распределения случайной величины ![]() . Если момент
. Если момент ![]() выбрать
произвольно, то одномерный закон распределения является функцией двух
аргументов:
выбрать
произвольно, то одномерный закон распределения является функцией двух
аргументов: ![]() и
и ![]() .
.
Характеристическая функция
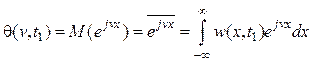 (4.2)
(4.2)
– преобразование Фурье от плотности вероятности, в равной степени описывает сечение процесса.
Наиболее полно процесс ![]() может быть представлен многомерной
(n-мерной) плотностью вероятности
может быть представлен многомерной
(n-мерной) плотностью вероятности![]() или многомерной характеристической функцией
или многомерной характеристической функцией
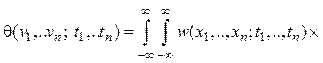
![]() . (4.3)
. (4.3)
Получение и исследование многомерных плотностей и характеристических функций представляет серьёзные трудности.
Во многих случаях оказывается возможным ограничиться более простыми характеристиками случайных процессов – их моментными функциями: начальными и центральными.
Начальные, или просто моментные функции ![]() -го порядка
-го порядка
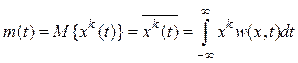 . (4.4)
. (4.4)
Центральные моментные функции ![]() -го порядка
-го порядка
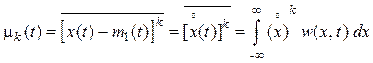 , (4.5)
, (4.5)
где ![]() ,
, ![]() .
.
Наиболее важными для практического использования являются моментные
функции первых двух порядков: математическое ожидание ![]() ,
среднее значение квадрата
,
среднее значение квадрата ![]() и дисперсия
и дисперсия ![]() , при этом
, при этом
![]() . (4.6)
. (4.6)
Количественной характеристикой скорости изменения случайных
процессов служат корреляционные моментные функции, устанавливающие статистическую
взаимосвязь значений процессов в различных сечениях (в моменты ![]() и
и ![]() ):
):
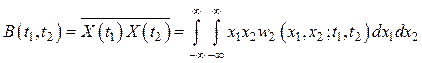 , (4.7)
, (4.7)
![]() , (4.8)
, (4.8)
называемые соответственно (авто) ковариационной и (авто) корреляционной функциями.
В практических приложениях часто рассматриваются так называемые стационарные
процессы. Если ![]() -мерный закон распределения не
изменяется при любом сдвиге
-мерный закон распределения не
изменяется при любом сдвиге ![]() всей группы сечений
вдоль оси времени, т. е. если он инвариантен относительно времени
всей группы сечений
вдоль оси времени, т. е. если он инвариантен относительно времени
![]() , (4.9)
, (4.9)
то случайный процесс называется стационарным в строгом или узком
смысле. Следовательно, двумерный и одномерный законы инвариантны относительно
времени. Моментные функции превращаются в моменты – числовые характеристики
закона распределения, т. е. ![]() ,
, ![]() ,
, ![]() и т.
д.
и т.
д.
Для определения моментов можно использовать также характеристическую
функцию ![]() :
:
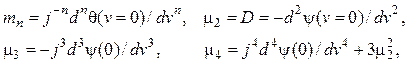 (4.10)
(4.10)
где ![]() – так называемая кумулянтная функция.
– так называемая кумулянтная функция.
Имеется ещё числовая характеристика законов распределения – так называемая энтропия, выражающая их неопределённость:
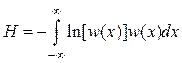 . (4.11)
. (4.11)
В рамках корреляционной теории (для моментов не выше второго
порядка) стационарность процесса определяется в широком смысле. Ограничиваются
требованием, чтобы математическое ожидание и дисперсия не зависели от времени,
а корреляционная функция определялась бы только интервалом ![]() , т. е.
, т. е. ![]() .
.
Для нормальных (гауссовых) процессов понятия стационарности в широком и узком смысле совпадают. Такие процессы исчерпывающим образом описываются указанием математического ожидания и АКФ.
Среди стационарных выделяют так называемые эргодические
процессы. Стационарный в узком смысле процесс называется эргодическим,
если любая вероятностная характеристика такого процесса, полученная путём
усреднения по ансамблю реализаций, равна временному среднему, полученному
усреднением за достаточно большой промежуток времени наблюдения ![]() из одной реализации. Для случайного процесса,
стационарного в широком смысле, условие эргодичности формулируется
относительно математического ожидания, дисперсии и корреляционной функции.
Следовательно,
из одной реализации. Для случайного процесса,
стационарного в широком смысле, условие эргодичности формулируется
относительно математического ожидания, дисперсии и корреляционной функции.
Следовательно,
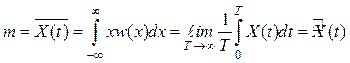 , (4.12)
, (4.12)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.