Основные характеристики случайных процессов, страница 5

.

36. Определите энтропию нормального шума ; плотность вероятности определяется выражением

.

37. Используя результат, полученный в задачах 35 и 36, найдите разность энтропии нормального и равномерного законов при одном и том же среднем квадратическом отклонении .

4.3.4. Спектральный и корреляционный анализы

38. Определите и изобразите графически СПМ  случайного процесса  по его корреляционной функции . Рассчитайте эффективную ширину спектра  и интервал корреляции  и .

39. Найдите и изобразите функцию корреляции  стационарного случайного процесса  со спектральной плотностью мощности  при . Определите также интервал корреляции  и .

40. Покажите, что корреляционная функция  не изменяется при добавлении к случайному процессу  детерминированной составляющей .

41. Заданы корреляционные функции:

а) ;

б) ;

в) .

Изобразите эти функции и рассчитайте интервал корреляции ,  (и  для функции “в”), а также эффективную ширину спектра .

42. Для стационарного случайного процесса

,

где  – случайная величина, определите корреляционную функцию как усреднением по ансамблю реализаций, так и по одной реализации на большом интервале наблюдения . Является ли процесс  эргодическим по отношению к корреляционной функции?

43. Найдите корреляционную функцию  и спектральную плотность мощности  “телеграфного сигнала”, заданного в задаче 24 (рис. 4.5). Изобразите графики  и .

44. По результатам предыдущей задачи рассчитайте интервал корреляции  и , а также эффективную ширину спектра .

45. Определите корреляционную функцию процесса

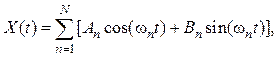
где  – известные частоты, а вещественные случайные величины  и  взаимно не коррелированы, имеют нулевые математические ожидания и дисперсии  .

4.3.5.  Узкополосные случайные процессы

46. Задан нормальный узкополосный случайный процесс

,                                  (*)

где  и  – медленные функции по сравнению с . Дисперсия . Найдите вероятность того, что в фиксированный момент времени огибающая  процесса  превысит уровень 2 В.

47. Для процесса вида (*) выразите математическое ожидание () и дисперсию () огибающей через его среднеквадратическое значение ().

48. Определите, является ли процесс вида (*) эргодическим относительно математического ожидания .

49. Выразите корреляционную функцию  процесса вида (*) через известную функцию корреляции  огибающей , приняв .

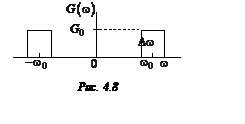
50. Найдите спектральную плотность мощности  узкополосного случайного процесса , если его корреляционная функция имеет вид

.

Изобразите графики  и .

51. По условию предыдущей задачи найдите и графически изобразите АКФ  и СПМ  огибающей  случайного процесса . Рассчитайте интервал корреляции  и эффективную ширину спектра  огибающей , если  1 В,  = 10⁴ 1/с.

52. Найдите корреляционную функцию  процесса вида , если спектральная плотность мощности равномерна в полосе частот  (рис. 4.8).

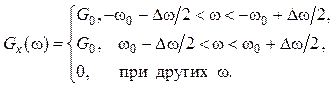
Изобразите график  и определите интервал корреляции  огибающей этой функции.

53. Определите эффективную ширину спектра стационарного узкополосного процесса  по его корреляционной функции

.

4.4.                Контрольное задание

4.4.1.  Вероятность превышения заданного уровня

На пороговую схему воздействует случайное напряжение, распределенное по нормальному закону

.

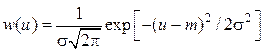Какова вероятность  срабатывания схемы в фиксированный момент времени (t₁), если схема срабатывает () всякий раз, когда напряжение на ее выходе превышает пороговое значение .

Параметры  и  даны в табл. 4.1, а  – в табл. 4.2.

Таблица 4.1

Параметр	Номер варианта
	0	1	2	3	4	5	6	7	8	9
, B	–0.5	0	0.5	1.0	1.5	–0.5	0	0.5	1.0	1.5
, B.	1.0	1.0	1.0	1.0	1.0	2.0	2.0	2.0	2.0	2.0

Таблица 4.2

Параметр	Номер варианта
	0	1	2	3	4	5	6	7	8	9
, B	–2.0	–1.5	–1.0	–0.5	0	0.5	1.0	1.5	2.0	2.5

    Методическое указание