![]()
Кафедра теоретических
основ радиотехники (ТОР)
Задание № 3
Закон распределения
Моментные функции. Стационарность и эргодичность
Факультет: РЭФ Вариант 6
Группа: РТ5-24 Подвариант 4
Студент: Доценко С.А.
Дата сдачи: "21" мая 2004
Преподаватель: Курилин И.В.
Новосибирск, 2004
Рабочее задание
4.4.2. Закон распределения
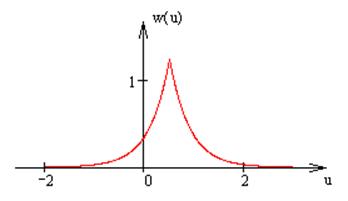
Стационарный случайный процесс U(t) описан плотностью вероятности w(u).
Требуется:
a) получить выражение для функции распределения F(u);
б) построить график F(u);
в) найти выражение для характеристической функции θ(ν) и энтропии Н.
4.4.3. Моментные функции. Стационарность и эргодичность
Задан процесс Z(t). При его описании приняты следующие обозначения:
S1(t), S2(t) – детерминированные функции времени, описываемые с помощью постоянных парметров S0, α, ω0, p, τ и n;
X и Y – некоррелированные случайные величины с известными математическими ожиданиями mx и my и дисперсиями Dx = σx2 и Dy = σy2;
X(t) и Y(t) – некоррелированные эргодические случайные процессы, которые соответственно имеют известные математические ожидания mx и my и дисперсии Dx = σx2 и Dy = σy2 и автокорреляционные функции Kx(τ) и Ky(τ).
Требуется:
а) определить математическое ожидание mz(t), дисперсию Dz(t) и корреляционную функцию Kz(t1, t2) процесса Z(t);
б) классифицировать процесс Z(t) по признакам стационарности и эргодичности.
Результаты выполнения задания
4.4.2. Закон распределения
Исходные данные
Плотность
вероятности имеет вид: ![]() , -∞ < u < ∞,
, -∞ < u < ∞,
где λ = 2.5 1/B, U0 = 0.5 B
(a) Функция распределения
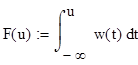
![]()
(б) График функции распределения
(в) Выражения для характеристической функции и энтропии
Выражение для нахождения характеристической функции:
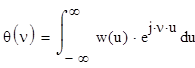
![]()
График характеристической функции
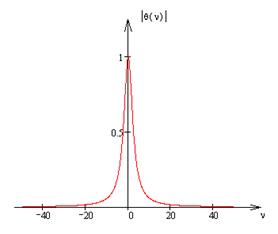
Выражение для вычисления энтропии:
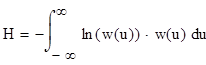
H = 0.777
Энтропия выражает неопределённость закона распределения.
4.4.3. Моментные функции. Стационарность и эргодичность
Исходные данные
Процесс: Z(t) = Ysin(ωt) + S2(t), где S2(t) = S0cos(ωt)
(а) Математическое ожидание, дисперсия и корреляционная функция процесса Z(t)
Математическое ожидание и дисперсия случайной величины Y:
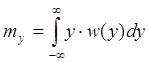 ,
, 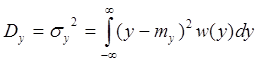
Эти величины по условию известны.
Математическое ожидание процесса
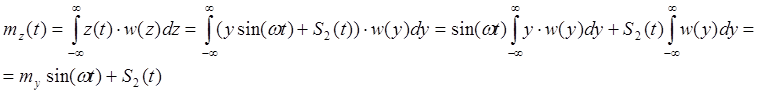
Были использованы свойства:
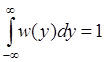 ,
,
S2(t) и sin(ωt) не зависят от y, поэтому их можно выносить за знак интеграла
Дисперсия процесса
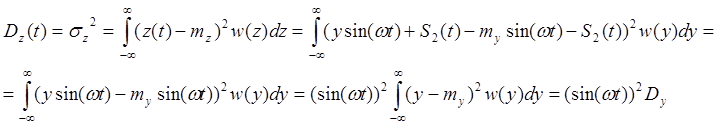
Корреляционная функция процесса
![]()
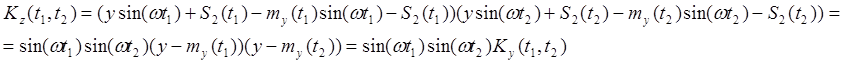
(б) Классификация процесса по признакам стационарности и эргодичности
Процесс называется стационарным (в широком смысле), если математическое ожидание и дисперсия не зависят от времени, а корреляционная функция зависит лишь от временного сдвига, но не от времени непосредственно.
В нашем случае мы получили:
![]() ,
,
![]() ,
,
где my и Dy – математическое ожидание и дисперсия некоррелированной
случайной величины Y, не зависящие от времени;
то есть математическое ожидание и дисперсия процесса явно зависят от времени.
Полученная
корреляционная функция процесса ![]() также явно зависит от
времени.
также явно зависит от
времени.
Итак, мы пришли к выводу, что ни одно условие стационарности процесса (в широком смысле) не выполнено, значит, исследуемый процесс нестационарен. Также процесс не является эргодическим, т.к. эргодический процесс – это разновидность стационарного процесса.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.