Другие предметы \ Радиотехнические цепи и сигналы

Спектральный анализ сигналов. Определение спектральной плотности сигнала. Дискретизация непрерывных сигналов

Страницы работы

10 страниц (Word-файл)

Посмотреть все страницы

Скачать файл

Уважаемые коллеги! Предлагаем вам разработку программного обеспечения под ключ.

Опытные программисты сделают для вас мобильное приложение, нейронную сеть, систему искусственного интеллекта, SaaS-сервис, производственную систему, внедрят или разработают ERP/CRM, запустят стартап.

Сферы - промышленность, ритейл, производственные компании, стартапы, финансы и другие направления.

Языки программирования: Java, PHP, Ruby, C++, .NET, Python, Go, Kotlin, Swift, React Native, Flutter и многие другие.

Всегда на связи. Соблюдаем сроки. Предложим адекватную конкурентную цену.

Заходите к нам на сайт и пишите, с удовольствием вам во всем поможем.

Содержание работы

Министерство образования Российской Федерации

НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра теоретических основ радиотехники (ТОР)

РАДИОТЕХНИЧЕСКИЕ ЦЕПИ И СИГНАЛЫ

РГЗ № 2

СПЕКТРАЛЬНЫЙ АНАЛИЗ СИГНАЛОВ

ДИСКРЕТИЗАЦИЯ НЕПРЕРЫВНЫХ СИГНАЛОВ

Вариант: 0

Подвариант: 6

Факультет: РЭФ

Группа: РТ5-91

Студент: Чебанов А.В.

Преподаватель: Яковлев А. Н.

Новосибирск 2011

Дано:

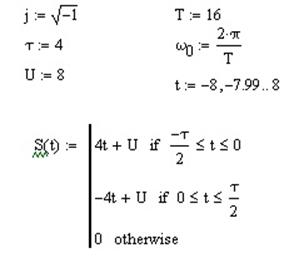
Безымянный.jpg

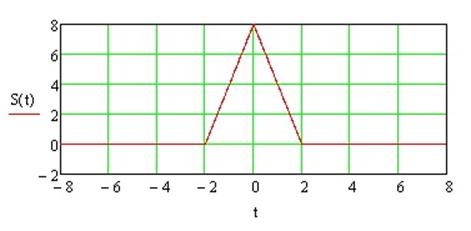
сигн.jpg

Построим график производной заданного сигнала:

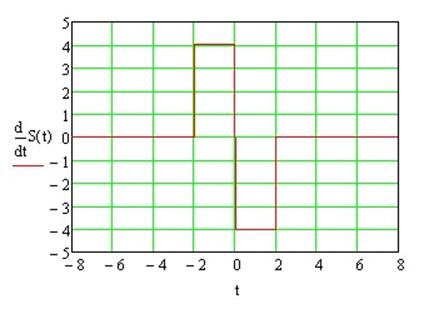
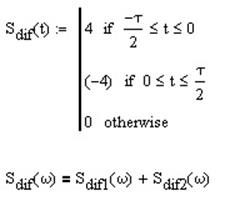
сигн1.jpg

Спектр дифферинцированного сигнала будет равен:

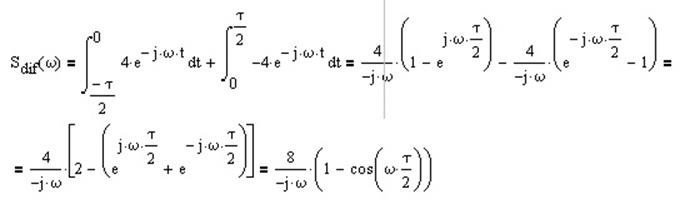
диф.jpg

Исходя из теоремы о спектре производной от сигнала:

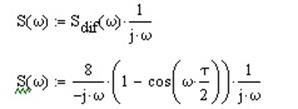
наш.jpg

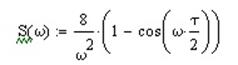
наш1.jpg

Запишем выражения для фазового спектра:

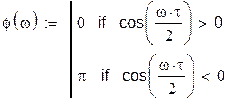
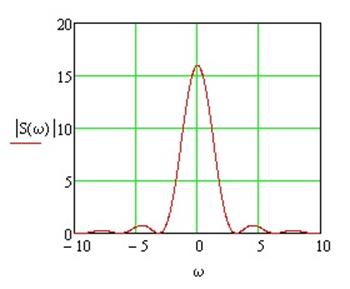
Спектральная диаграмма модуля

диаг.jpg

Диаграмма фазы

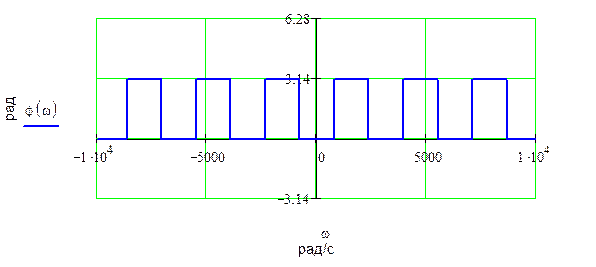
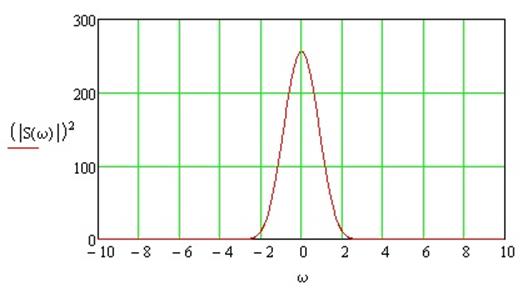
Диаграмма энергетического спектра:

диаг1.jpg

Ширину лепестка сигнала определяем по спектральной диаграмме модуля .

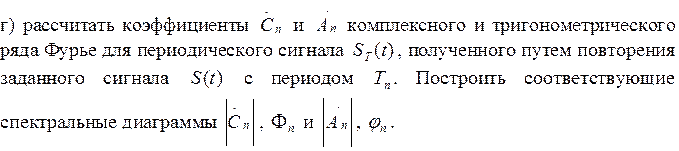
Так как сигнал четный, следовательно, коэффициенты b_n=0.

Найдем коэффициенты a_n_:

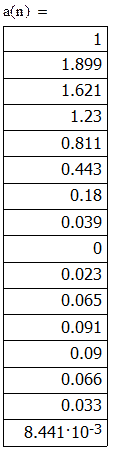
Найдем коэффициенты A_n:

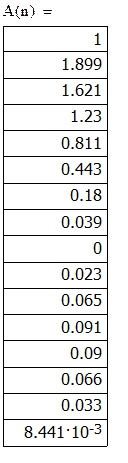
Запишем выражение для фазы периодического сигнала:

спектральная диаграмма тригонометрического ряда Фурье для периодического сигнала

диаграмма фазы периодического сигнала

Запишем выражение для коэффициентов комплексного ряда Фурье

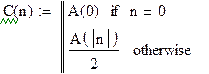
Выражение для фазы комплексного ряда Фурье периодического сигнала:

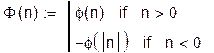
Спектральная диаграмма коэффициентов

Спектральная диаграмма фазы

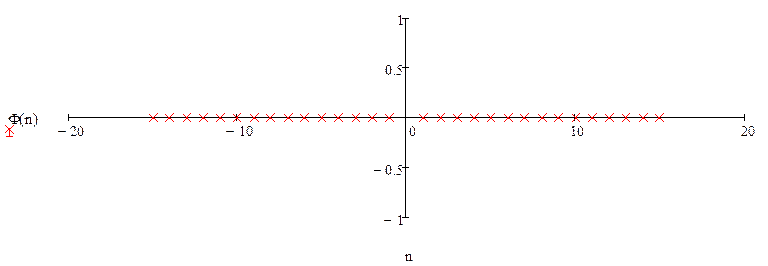
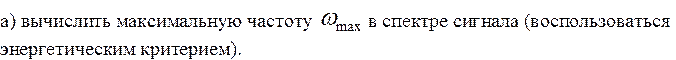
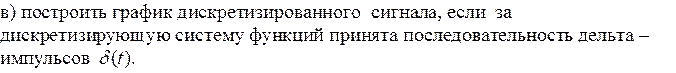
Запишем заданный сигнал S(t) с помошью функций Хевисайда:

интервал дискретизации

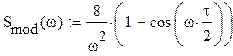
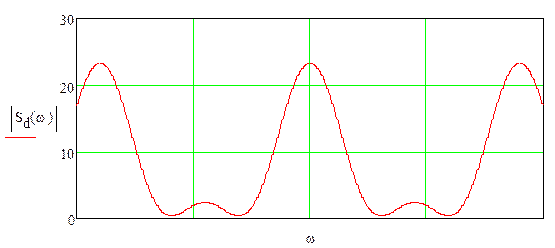
спектральная плотность дискретизированного сигнала

ЛИТЕРАТУРА

1. Радиотехнические цепи и сигналы. Задачи и задания. Учеб. пособие / Коллектив авторов; под ред. проф. А.Н. Яковлева. – М.: ИНФРА-М; Новосибирск: Изд-во НГТУ, 2003. – 348 с. (Серия «Высшее образование»).

2. Конспект лекций по курсу РТЦиС .