Амплитудная модуляция, страница 4

                    .                     (7.21)

.

На выходе блока вычитания из первого тока вычитается второй:

.                                             (7.22)

Если и , то из (7.22) следует

.          (7.23)

Фильтр Ф подавляет низкочастотную составляющую  и на его выходе получается колебание БМ, т.е. сигнал ДБП:      

 .                      (7.24)

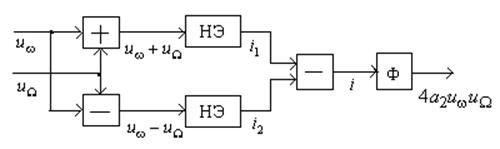
Рис.7.15

            В качестве НЭ можно использовать транзисторы и, в простейшем случае, полупроводниковые диоды. Схема диодного БМ приведена на рис. 7.16, а на рис.7. 17 – сигнал ДБП при тональной модуляции.

                               Рис. 7.16                                                  Рис.7.17

         Схему рис.7.17. можно дополнить двумя диодами (рис. 7.18), что позволит освободиться от составляющей  и, следовательно, от фильтра Ф – колебательного контура. Выражения для тока новой пары диодов Д3 и Д4:

 =

= .                                                     (7.25)

Сложение выражений (7.22) и (7.25) дает

.             (7.26)

Схема, представленная на рис. 7.18 называется кольцевым модулятором. А ней все четыре диода включены в одно кольцо (рис. 7.18, а). Она удобна не только тем, что не требуется колебательный контур, но  она подавляет паразитные составляющие типа , возникающие при аппроксимации ВАХ  НЭ полиномом третьей степени и создающие нелинейные искажения.

Таким образом, при одинаковых диодах и небольших амплитудах сигналов и , когда ВАХ диодов можно аппроксимировать квадратичным или кубичным полиномом, кольцевой модулятор является идеальным перемножителем-преобразователем двух входных сигналов. Спектр выходного сигнала содержит только боковые составляющие с частотами .

Такие кольцевые преобразователи нашли широкое применение не только в качестве модуляторов, но детекторов, преобразователей частоты, а также используются в измерительной технике.

а

б

Рис. 7.18

7.5. Амплитудная модуляция с использованием АПС

Схема модулятора показана на рис. 7.19. В простейшем случае пусть поданы на входы Х и Y  напряжения

,   .

Тогда на выходе АПС будет

 = , где

                      ,    .                                 (7.27)

Изменяя амплитуду управляющего сигнала  и/или величину смещения , можно в широких пределах изменять коэффициент модуляции  М: от нуля до бесконечности.

На рис. 7.20, а приведен график зависимости , а на рис. 7.20, б –  временные диаграммы для различных значений . В частном случае, когда = 0, имеем

=  , т.е. получается модуляция с подавленной несущей составляющей (иногда ее называют балансной модуляцией).

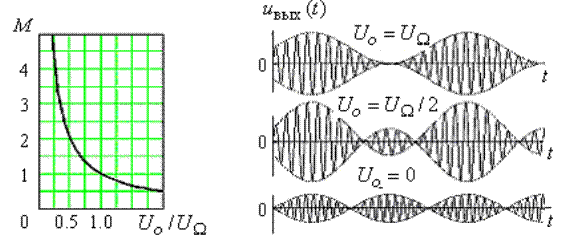
а                                        б

Рис. 7.20

7.6. Однополосная модуляция

Модуляция, в результате которой получается сигнал с одной боковой полосой (ОБП), называется однополосной модуляцией (ОМ).

Достоинства ОМ по сравнению с обычной модуляцией:

– отсутствие потерь мощности на передачу несущей частоты (как и в случае ДБП) и одной боковой полосы. Это позволяет увеличить мощность передаваемой боковой полосы и, следовательно, дальность системы связи;

– как и при ДБП не расходуется мощность в режиме молчания (при отсутствии модулирующего сигнала);

– более узкая занимаемая полоса частот, что позволяет увеличить число радиостанций (каналов связи) в заданном диапазоне частот;

– более узкая полоса пропускания приемного  тракта, что позволяет снизить уровень помех на входе приемного устройства.

Недостатки. Связь с использованием сигналов ОБП осуществляется за счет усложнения передающего и приемного устройств. В приемнике необходимо восстановить несущее колебание, синхронизировать его с несущим, но подавленным колебанием передатчика.

Формирование сигнала ОБП осуществляется:

– методом фильтрации;

– методом фазирования.

Идея метода фильтрации поясняется на рис. 7.21. Сначала с помощью БМ формируется  сигнал ДБП. Далее ставится полосовой фильтр (ПФ), пропускающий на выход сигнал одной боковой полосы (верхней или нижней). Фильтрация будет тем лучше, чем больше полоса отчуждения. При отсутствии полосы отчуждения, например в спектре телевизионного сигнала, метод фильтрации неприменим.

Рис. 7.21