Амплитудная модуляция, страница 2

Из (7.7) и (7.8) следует, что модулятор можно рассматривать как резонансный усилитель с управляемой крутизной, т.е. как параметрическую цепь.

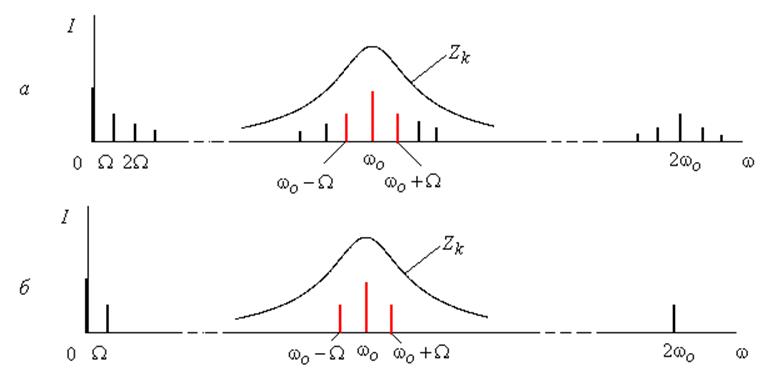
Рис.7.6

Таким образом, глубина модуляции тока  тем больше, чем больше амплитуда модулирующего сигнала  и чем сильнее нелинейность ВАХ, определяемая коэффициентом . Изменение огибающей  пропорционально модулирующему сигналу , поэтому модуляция оказывается неискаженной.    

На практике рабочий участок ВАХ  НЭ модулятора выбирают по статической модуляционной характеристике. Это зависимость амплитуды тока первой гармоники  НЭ или напряжения на выходе модулятора  от напряжения смещения  при подаче на вход гармонического несущего колебания с постоянной амплитудой  (рис. 7.7)

, , .                                      (7.9)

Часто статическую модуляционную характеристику определяют графоаналитически по известной ВАХ НЭ и заданной амплитуде входного сигнала U_m: для каждого смещения определяют по методу трех ординат амплитуду тока .

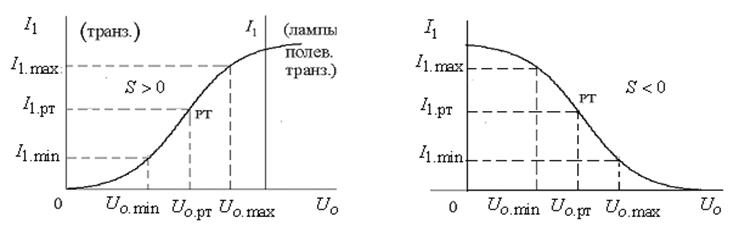
Рис. 7.7

В случае аппроксимации ВАХ степенным полиномом она находится из выражения (7.5)  при:

.                             (7.10)

Для квадратичного участка ВАХ, когда , эта характеристика линейна

                                                               (7.11)

и, как уже отмечалось, нелинейные искажения огибающей отсутствуют.

Статическая модуляционная характеристика позволяет выбрать рабочий участок ВАХ НЭ, необходимый для неискаженной амплитудной модуляции (, ), и определить для этого участка:

1. Максимально возможный коэффициент АМ по току

           .

2. Рабочее напряжение смещения (рабочую точку)

.

3. Максимальную амплитуду управляющего напряжения

.

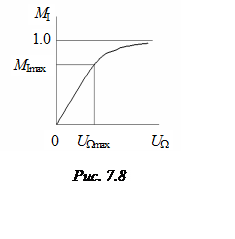
Динамическая модуляционная характеристика (рис. 7.8) – это зависимость коэффициента модуляции M_I  от амплитуды модулирующего сигнала  при постоянных смещении  и амплитуде ВЧ колебаний , т.е.

, , .                              (7.12)

Эта характеристика может быть рассчитана по статической модуляционной характеристике (если для обеих взяты одинаковые ) или на основе формул (7.5), (7.7). По формулам определяют зависимости максимального и минимального мгновенных значений тока первой гармоники (, ) от амплитуды модулирующего  напряжения   для  известных  (заданных)  , .

Следовательно

 .         (7.13)

Аппроксимация ВАХ НЭ кусочно-линейной зависимостью

При больших амплитудах  входного ВЧ колебания ВАХ НЭ  можно  аппроксимировать  кусочно-линейной зависимостью. Тогда амплитуда тока первой гармоники и, следовательно, статическая модуляционная характеристика запишется

                        (7.14)

где  – амплитуда импульсов тока, линейно зависящая от напряжения смещения . При подаче модулирующего колебания смещение будет изменяться во времени  и, следовательно, амплитуда импульсов тока будет пропорционально изменяться от управляющего напряжения (рис.7.8)

.

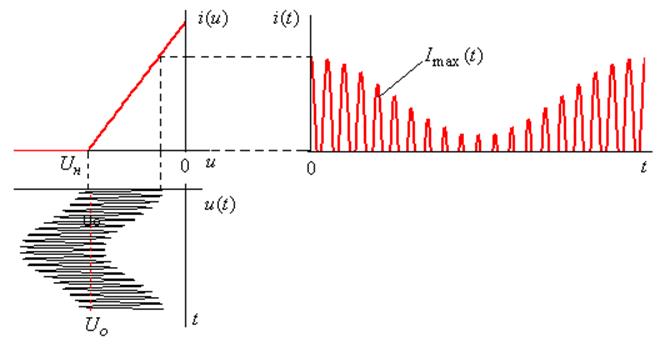
Рис. 7.8

Для того чтобы амплитуда тока первой гармоники  прямо пропорционально изменялось с изменением (под воздействием  модулирующего сигнала), необходимо постоянство сомножителя  в формуле (7.14). Это обеспечивается в диапазоне углов отсечки

 ;                                                  (7.15)

при этом  . При выполнении условия (7.15) выражение (7.14) запишется

, т.е. АМ будет без нелинейных искажений.

7.3. Линейные искажения

Воспользуемся спектральным (гармоническим) методом анализа. При отсутствии нелинейных искажений спектр тока будет выглядеть так, как показано на рис. 7.9, а. Полезные компоненты тока (при ):

, где  – амплитуда тока на боковых частотах .

Нагрузкой НЭ служит колебательный контур (с неполным включением), сопротивление которого зависит от частоты:

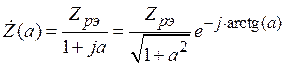
где  – обобщенная расстройка контура, – резонансное сопротивление контура при неполном включении, – коэффициент включения, – резонансное сопротивление контура,  – характеристическое сопротивление контура,  и  – добротность и сопротивление потерь контура. АЧХ и ФЧХ контура

,

.

Первый случай. Контур настроен на несущую частоту, т.е. . АЧХ и ФЧХ контура приведены на рис. 7.9, б.    Найдем отклик контура на каждую составляющую тока:

на частоте  

,   на частоте  

, на частоте  

, где , ,  и  – сопротивление и фазовый сдвиг контура на боковых частотах.