Амплитудная модуляция, страница 3

Спектральные диаграммы амплитуд и фаз напряжения на контуре приведены на рис. 7.9, в, г.

Результирующее напряжение на контуре и, следовательно, выходное напряжение запишем в виде

= ++ =

= ,                                         (7.16)

где

                                     ,                                         (7.17)

.                                                        (7.18)

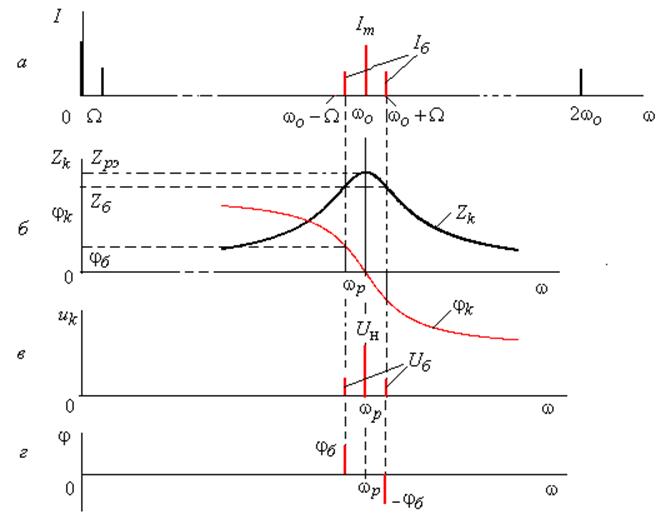
Рис. 7.9

Из всего изложенного можно сделать выводы.

Во-первых, происходит уменьшение глубины модуляции по напряжению  по сравнению с глубиной модуляции по току .

Коэффициент , определяющий ослабление глубины модуляции

                         (7.19)

зависит от частоты . График зависимости  приведен на рис. 7.10 и повторяет правую ветвь резонансной кривой контура. Чем больше добротность контура  (уже полоса пропускания ), тем меньше величина , т.е. тем сильнее ослабление модуляции.

Во-вторых, происходит запаздывание огибающей выходного напряжения на угол  (время ). Это наглядно поясняется с помощью векторных диаграмм (для ), приведенных на рис. 7.11. Из векторной диаграммы напряжений следует, что должно пройти некоторое время , чтобы боковые векторы повернулись на угол , и лишь только тогда результирующий вектор  достигнет максимального значения. Чем больше добротность контура , тем больше угол  и тем больше задержка  огибающей напряжения.

Таким образом в рассматриваемом случае следует, что линейные искажения заключаются в ослаблении модуляции и задержке огибающей напряжения относительно огибающей тока (рис. 7.12). Поэтому чем меньше добротность контура , тем меньше линейные искажения. Но при этом уменьшается амплитуда выходного напряжения  из-за снижения резонансного сопротивления контура .

При модуляции сложным видеосигналом (рис. 7.3), для уменьшения линейных искажений надо иметь контур с достаточной полосой пропускания

                                                .                                             (7.20)

              Второй  случай. Контур расстроен относительно несущей частоты, т.е. . Выясним особенности этого случая. АЧХ и ФЧХ контура смещены относительно спектра тока (рис. 7.13. а, б). Поэтому спектр напряжения будет несимметричным (рис. 7.13, в, г) относительно несущей частоты : амплитуда составляющей  верхней боковой частоты будет больше составляющей  нижней боковой частоты, а их фазовые сдвиги, наоборот, т.е.  (на рис.7.13, г ). Напряжение несущей частоты уменьшится из-за расстройки контура и будет сдвинуто относительно тока этой частоты на угол .

Векторные диаграммы тока и напряжения приведены на рис. 7.14 (для ). Результирующий вектор напряжения  сдвинут относительно вектора несущего напряжения  на угол .

Временная зависимость  может быть получена на основании векторных диаграмм, построенных для ряда моментов времени, либо путем суммирования мгновенных значений всех рех составляющих напряжения.

Анализируя результат можно в качестве выводов выявить следующие особенности линейных искажений  в рассматриваемом случае.

Во-первых, длина вектора , изображающего результирующее напряжение, будет изменяться во времени по сложному закону, не совпадающему с гармоническим.

Во-вторых, возникает модуляция по фазе .

В-третьих, глубина модуляции по напряжении. Может возрасти

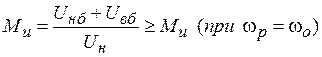
так как сумма боковых составляющих почти не изменилась за счет увеличения  и уменьшения , а амплитуда несущего напряжения  уменьшилась.

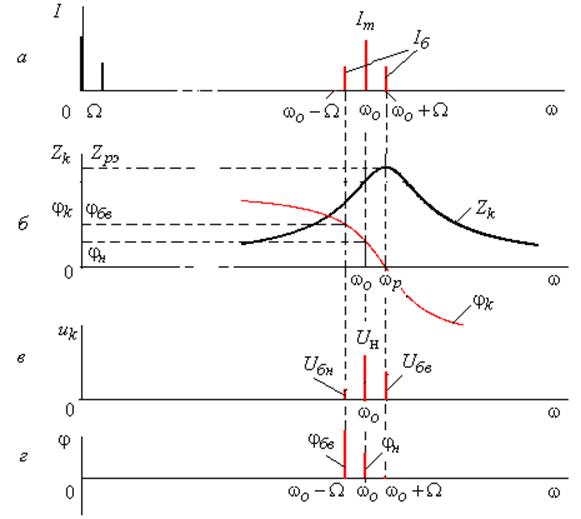
Рис.7.13

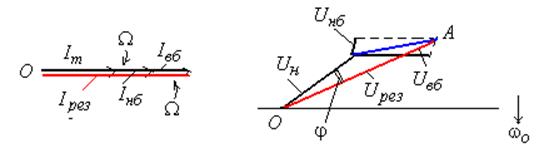
Рис.7.14

После детектирования в приемнике выделится огибающая АМК, которая искажена по сравнению с огибающей тока. Поэтому на выходе детектора приемника получится искаженная информация (по сравнению с переданной).

7.4. Балансная модуляция

В первой части курса было установлено, что при передаче модулированного сигнала  с подавленной несущей частотой, т.е. сигнала с двумя боковыми полосами (ДБП), можно получить значительный выигрыш в мощности.

Для получения сигналов ДБП применяются балансные модуляторы (БМ). Действие БМ основано на компенсации напряжения несущей частоты при сложении двух амплитудно-модулированных колебаний (АМК) на общей нагрузке. Структурная схема БМ приведена на рис.7.15. На первый НЭ подается сумма модулируемого и модулирующего сигналов , а на второй НЭ – разность . Пусть оба НЭ одинаковы и их ВАХ аппроксимированы полиномом второй степени: