Учебное пособие по курсу "Радиотехнические системы", страница 3

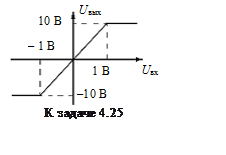
4.25. В многоканальной системе с ЧРК одновременно передаются 50 телефонных сообщений с помощью частотной модуляции. Амплитуда каждого сигнала 60 мВ. Найти вероятность неискаженного прохождения группового сигнала через усилитель с характеристикой, показанной на рисунке.

4.26. Радиопередатчик автоматической станции имеет ресурс непрерывной работы 100 часов, ограниченный автономным источником энергии станции. Передатчик может работать с любым видом манипуляции: АТ, ЧТ, ФТ. Допустимая вероятность ошибки на символ 10^–5. Выбрать вид манипуляции, обеспечивающий передачу автоматической станцией наибольшего (максимального) количества информации.

5. ЦИФРОВАЯ МОДУЛЯЦИЯ И КОДИРОВАНИЕ

В СИСТЕМАХ СВЯЗИ

5.1. Определить вероятность ошибки в 12-битовом слове данных, кодированном линейным блочным кодом (24, 12). Вероятность ошибки в канальном двоичном символе равна 10^–3.

5.2. Рассчитать уменьшение вероятности ошибки в слове данных, кодированном линейным блочным кодом (24, 12), по сравнению с некодированной передачей при использовании когерентной BPSK, при  = 10 дБ.

5.3. Минимальное расстояние для конкретного линейного блочного кода равно 11. Найти максимальные возможности кода по обнаружению и исправлению ошибок.

5.4. При передаче сигнала используется DPSK. Скорость передачи информационных двоичных символов составляет 10 кбит/с. Используется кодирование (7, 4). Достаточно ли значение отношения средней мощности сигнала к СПМ шума на входе  = 48 дБ·Гц для получения вероятности ошибки  на выходе декодера?

5.5. Задана матрица генератора линейного блочного кода (7, 4) следующего вида:

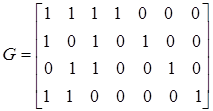
Найти: а) все кодовые слова кода; б) проверочную матрицу  этого кода; в) синдром для принятого слова 1101101; г) возможности кода по обнаружению и исправлению ошибок.

5.6. Определить, какие из следующих полиномов могут генерировать циклический код с кодовым словом длиной < = 7: а)            б)       в)  

г) 1 + Х + Х² + Х⁴;     д) .

Найти значение () для каждого из таких кодов.

5.7. Сконструировать кодер на регистре сдвига с обратной связью для циклического систематического кода (8, 5) с генератором . С его помощью закодировать сообщение 10101.

5.8. Код БЧХ (63, 36) может исправлять пять ошибок. Девять блоков (7, 4) того же кода могут исправлять девять ошибок. Степень кодирования в обоих вариантах одинакова. Является ли код (7, 4) более мощным? Сравнить оба кода, когда наблюдается пять ошибок в 63 битах сообщения.

5.9. Исходная информационная последовательность разбивается на 36 битовых слов и передается по каналу АБГШ с использованием BPSK. Рассчитать , необходимое для обеспечения вероятности ошибки в слове, равной  10^–3, без использования кодирования. Рассчитать эффективность кодирования при использовании линейного блочного кода (127, 36) для того же значения вероятности ошибки в слове данных.

5.10. Последовательность данных кодируется кодом БЧХ (127, 64), а затем моделируется с использованием когерентной 16-ричной PSK. Отношение  = 10 дБ на входе системы. Присвоение символам модулятора битового значения осуществляется с использованием кода Грея. Найти вероятность ошибки в принятом символе и кодовом двоичном символе и двоичном информационном символе. Для полученной ошибки в информационном  двоичном символе определить требуемое отношение , если воспользоваться вместо указанной модуляции 16-ричной когерентной ортогональной FSK.

5.11. Последовательность двоичных данных разбивается на блоки по 5 бит и кодируется с использованием матрицы Адамара. Для требуемой вероятности битовой ошибки  найти эффективность кодирования при побитовой передаче данных с использованием BPSK. Найти отношение  требуемое для обеспечения той же битовой ошибки с использованием 32-позиционной MFSK.

5.12. Нарисовать диаграмму состояний, древовидную и решетчатую диаграммы для кода со степенью кодирования 1/3 при  = 3, который имеет следующие генераторы: ,  и .