Учебное пособие по курсу "Радиотехнические системы", страница 11

8.11. На рисунке изображены отрезок цифрового сообщения и моменты тактовой синхронизации, запаздывающие на время  относительно точек точной синхронизации. Это приводит к снижению выходного эффекта коррелятора. Определить потери энергетического потенциала (в децибелах), вызванные этим эффектом, при приеме бита № 3 и бита № 4, если ошибка синхронизации  изменяется в пределах от 0,02T до 0,25T.

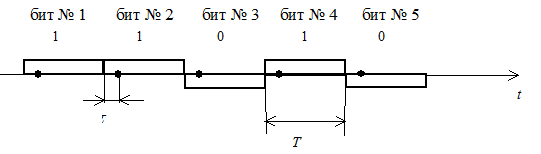
К задачам 8.10 и 8.11

8.12. На рисунке показаны отрезок цифрового сообщения и опережающие на время t моменты тактовой синхронизации. Определить потери (в децибелах) энергетического потенциала системы, вызванные неидеальностью синхронизации при демодуляции бита № 2 и бита № 3 и изменении t в диапазоне (0,05…0,2)Т.

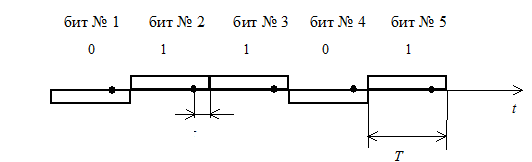
К задачам 8.12 и 8.13

8.13. Моменты тактовой синхронизации, показанные на рисунке точками, опережают на t время правильной синхронизации. Определить вызванное этим снижение отношения сигнал/шум (в децибелах) на выходе корреляционного приемника при приеме битов № 4 и № 5, если t изменяется в пределах (0,01…0,15)T.

8.14. Случайная ошибка t тактовой синхронизации подчиняется гауссовскому распределению с нулевым математическим ожиданием и дисперсией . Передача цифровой информации осуществляется при помощи когерентной амплитудной телеграфии. Энергия бита равна 10^–15 Дж, СПМ помехи – белого шума – 10^–16 Вт/Гц. Рассчитать зависимость вероятности ошибок демодуляции от значения  при приеме бита № 4 (см. рисунок к задачам 8.12 и 8.13), если , где T – длительность передачи одного бита информации.

8.15. Передача цифровой информации осуществляется при помощи фазовой телеграфии. Случайная ошибка t тактовой синхронизации подчиняется гауссовскому распределению с нулевым математическим ожиданием и дисперсией . Энергия бита равна 2·10^–15 Дж, СПМ помехи – белого шума – 2 · 10^–15 Вт/Гц. Рассчитать зависимость вероятности ошибок демодуляции от значения  при приеме бита № 4 (см. рисунок к задачам 8.12 и 8.13), если , где T – длительность передачи одного бита информации.

8.16. Случайная ошибка τ тактовой синхронизации подчиняется гауссовскому распределению с нулевым математическим ожиданием и дисперсией . Передача цифровой информации осуществляется при помощи относительной фазовой телеграфии. Энергия бита равна Дж, СПМ помехи – белого шума – 10^–16 Вт/Гц. Рассчитать зависимость вероятности ошибок демодуляции от значения  при приеме бита № 3 (см. рисунок к задачам  8.10 и 8.11), если , где T – длительность передачи одного бита информации.

8.17. Передача цифровой информации осуществляется при помощи когерентной частотной телеграфии. Случайная ошибка τ тактовой синхронизации подчиняется гауссовскому распределению с нулевым математическим ожиданием и дисперсией . Энергия бита равна 0,5 · 10^–14 Дж, СПМ помехи – белого шума – 0,4·10^–15 Вт/Гц. Рассчитать зависимость вероятности ошибок демодуляции от значения  при приеме бита № 4 (см. рисунок к задачам 8.10 и 8.11), если , где T – длительность передачи одного бита информации.

8.18. В цифровой системе связи с симметричными источниками информации (р₁ = р₀ = 0,5) для цикловой синхронизации в каждом слове используется однобитовая вставка. Длина слова n = 10 бит, число анализируемых слов при установлении цикловой синхронизации , порог установления синхронизации l = 4. Определить вероятность установления ложной синхронизации Р_лс.

8.19. Определить порог  установления цикловой синхронизации в приемнике цифровой системы связи, при котором вероятность ложной синхронизации не превысит Р_лс = 0,1. Длина двоичного слова в канале связи n = 15, количество слов, используемых для вхождения в режим синхронной связи, g = 10, среднее число 1 и 0 одинаково.

8.20. В системе цифровой связи используется помехоустойчивый «код с постоянным весом 3 из 7», при котором длина двоичного слова n = 7, а р₁ = 3/7. Число слов, используемых при вхождении в режим цикловой синхронизации, g = 12, порог установления синхронного режима l = 10. Какова вероятность возникновения ложной цикловой синхронизации Р_лс?