Средства связи с подвижными объектами, страница 6

Таким образом, корреляционные свойства М-последовательностей играют очень важную роль, поскольку они определяют как помехоустойчивость систем связи, так и возможность создания других систем последовательностей путем дополнительных преобразований.

2.3.2.  Корреляционные свойства М-последовательностей

При вычислении корреляционной функции (КФ)  дискретных сигналов  и  выполняется их поэлементное перемножение (причем, один из них берется со сдвигом на тактовых интервалов), суммирование и деление на число слагаемых (нормировка):

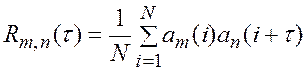.                                     (10)

Количество слагаемых в случае М-последовательностей равняется их длине  и является нечетной величиной. Поскольку перемножаемые числа при  равняются 1 или –1, то и отдельные произведения, входящие в (10), также равняются 1 или –1. В силу нечетности числа слагаемых сумма не может быть равной нулю. Из этого следует, что для взаимной корреляционной функции (ВКФ) различных М-последовательностей  и  всегда , т.е. различные М-последовательности не являются ортогональными функциями. При вычислении автокорреляционной функции (АКФ) =, поэтому в точке  сумма произведений равняется , откуда следует .

Необходимо иметь в виду, что КФ одиночных (непериодических) и периодических М-последовательностей различны. В случае одиночных сигналов  и  при  лишь  слагаемых в (10) отличны от нуля. При периодически повторяющихся же последовательностях все N парных произведений не равны нулю. Очевидно, результаты суммирования различаются между собой, что имеет место как для АКФ, так и для ВКФ.

На рис.7 приведены примеры корреляционных функций непериодических, а на рис.8 – периодических М-последовательностей. Эти примеры соответствуют М-последовательностям, генераторы которых представлены на рис.5 и 6, в дальнейшем для краткости называемым соответственно первой и второй М-последовательностями. Здесь – АКФ первой и второй последовательностей, а - их ВКФ. Характерной чертой непериодических последовательностей является равенство нулю АКФ и ВКФ при сдвигах . В отличие от этого КФ периодических последовательностей также периодичны с периодом равным N. На рис.8 периодические продолжения КФ показаны штриховыми линиями. Как и у всех сигналов АКФ М- последовательностей – четные функции, а ВКФ таким свойством не обладают. АКФ всех периодических М-последовательностей одинаковы (при их равной длине N), что отражено на рис.8-а. Их характерной чертой является постоянный уровень вне пикового значения, равный . Уровень боковых лепестков АКФ непериодических последовательностей более высок, его приближенно оценивают числом .

При N=7 имеем , . Как видно из рис.7-в и 8-б, ВКФ имеет еще большие значения, что отрицательно сказывается при всех применениях М-последовательностей, в том числе и в многостанционных системах связи со свободным доступом.

Относительно высокий уровень нежелательных выбросов корреляционных функций М-последовательностей является их недостатком. Зависимость же этого уровня от длины последовательности объясняет стремление к использованию длинных М-последовательностей.

Анализируя работу генераторов М-последовательностей, примеры которых приведены на рис.5 и 6, нетрудно прийти к выводу, что при изменении начального состояния регистра мы не изменим вида генерируемой периодической последовательности, а лишь осуществим ее временной сдвиг. При этом не изменятся и КФ периодических М-последовательностей. Этого нельзя сказать о непериодических (одиночных) М-последовательностях и их корреляционных функциях. Так если вместо второй М-последовательности использовать последовательность, получаемую в результате ее сдвига

,                                            (11)