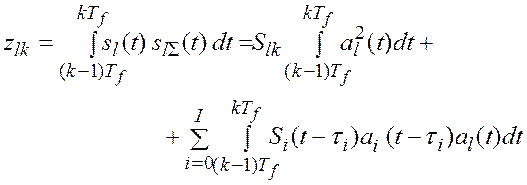Средства связи с подвижными объектами, страница 3

.                  (6)

Первый из двух интегралов в выражении (6) пропорционален энергии сигнала,

которую далее примем равной единице. Второе слагаемое описывает воздействие взаимной помехи, для которой характерно отсутствие синхронизации, поэтому каждый из  I  источников этой помехи имеет индивидуальный временной сдвиг  относительно опорного сигнала. На эту величину сдвинуты как адресные сигналы, так и соответствующие информационные сигналы. Отсюда следует, что в образовании выходного эффекта от воздействия i-й помехи участвуют два соседних значения сообщения i-го канала . Таким образом, функция  на интервале интегрирования претерпевает, возможно, однократное изменение своего значения, если указанные соседние значения не совпадают друг с другом. С другой стороны, адресные функции  и  являются быстроизменяющимися. Именно это определяет основные свойства отклика приемника на воздействие взаимной помехи, поэтому, полагая далее для простоты значения  одинаковыми, представим отклик приемного устройства (6) в следующем виде:

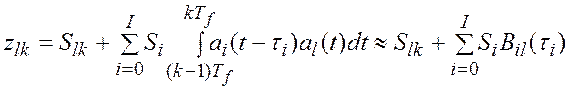,            (7)

где

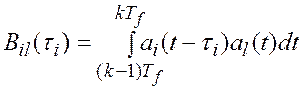 -                                   (8)

значение взаимной корреляционной функции l-го и i-го адресных сигналов, нормированное к энергии полезного сигнала в силу принятого предположения о равенстве единице отклика приемника на собственный адресный сигнал.

Таким образом, согласно (7), интенсивность взаимной помехи при приеме в системе связи со свободным доступом к каналу определяется свойствами функций взаимной корреляции всех пар адресных сигналов, используемых в ААСС. Для обеспечения высокого качества связи требуется, чтобы значения этих взаимно-корреляционных функций (ВКФ) при любых временных сдвигах были как можно меньшими. При условии достаточной малости отдельных слагаемых, входящих в сумму в правой части (7), даже при значительном числе I этих слагаемых общий уровень взаимной помехи может быть относительно невелик, что и обеспечивает работоспособность ААСС. Первостепенное значение при этом играют свойства кодовых последовательностей, применяемых в качестве адресных сигналов. В данной работе в роли кодовых последовательной изучаются так называемые последовательности максимальной длины или М-последовательности и коды Голда.

2.3.  М-последовательности и коды Голда

2.3.1.  Принципы формирования М-последовательностей

Для формирования ФМ-сигналов часто прибегают к использованию рекуррентных кодов, одной из разновидностей которых являются последовательности максимальной длины, получившие название М-последовательностей. Общий принцип рекуррентности заключатся, как известно, в том, что при вычислении любого элемента последовательности используется определенное количество ее же ранее сформированных элементов. Пусть  - рекуррентная кодовая последовательность, элементы которой принимают значения 1 или 0. Тогда рекуррентное соотношение, описывающее способ получения этой последовательности, имеет вид:

,                               (9)

где суммирование выполняется по модулю 2.

Согласно (9) текущий i-й элемент последовательности  вычисляется путем линейного преобразования n ранее сформированных элементов этой же последовательности. При этом используются n коэффициентов , значениями которых являются также 0 или 1. Если коэффициент , то соответствующий элемент последовательности  принимает участие в формировании текущего элемента  (т.е. входит в сумму правой части (9)), в случае же  элемент  в правой части (9) фактически отсутствует. Другими словами, конкретный набор коэффициентов  устанавливает, какие именно из n предыдущих элементов последовательности  принимают участие в формировании текущего элемента. Параметр n, имеющий смысл глубины рекурсии, называется порядком рекуррентного соотношения (9). Это соотношение полностью определяется набором своих коэффициентов , поэтому для обозначения последовательности обычно просто приводят этот набор. Иногда в его состав на первом месте включается значение , чем учитывается наличие в левой части (9) текущего значения  формируемой последовательности. В рабочей программе лабораторной работы коэффициент  не указывается, т.к. в работе генераторов он не участвует. Это необходимо иметь в виду при выполнении лабораторного задания.