Передаточная функция замкнутой системы. Передаточная функция ошибки от регулирующего воздействия

ЗАДАНИЕ НА РАБОТУ

1. По имеющейся в исходных данных передаточной функции разомкнутой системы записать передаточную функцию замкнутой системы.

2. Записать передаточную функцию для ошибки от регулирующего воздействия.

3. Изобразить структурную схему исследуемой системы, считая систему следящей.

4. Записать характеристические полиномы разомкнутой и замкнутой системы.

5. Исследовать систему на устойчивость по критерию Гурвица.

6. Исследовать систему на устойчивость по критерию Михайлова методом чередующихся корней.

7. Построить годограф Михайлова с указанием масштабов по обеим осям.

8. Исследовать систему на устойчивость по критерию Найквиста.

9. Построить годограф Найквиста с указанием масштабов по обеим осям.

10. Определить запас устойчивости по модулю и по фазе.

11. Вычислить коэффициенты ошибки и найти ошибку регулирования системы в установившемся режиме ξ(t) при заданной входной функции.

12. Построить график ξ(t) в масштабе по обеим осям.

ИСХОДНЫЕ ДАННЫЕ

Структура системы: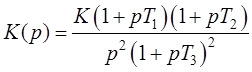         

Входное воздействие:     

Численные значения коэффициентов

6	0.05	2	0.02	0.1	-5	1.5	2	1

1. Передаточная функция замкнутой системы.

Для следящих систем (т.е. систем, для которых передаточная функция канала обратной передачи равна 1) передаточная функция замкнутой системы определяется как:

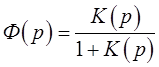                                                   (1.1)

Подставим в выражение (1.1) заданную передаточную функцию разомкнутой системы:

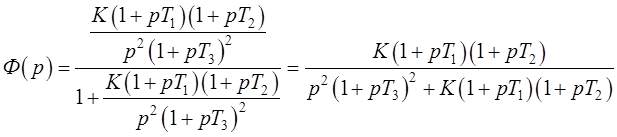           (1.2)

2. Передаточная функция ошибки от регулирующего воздействия.

Передаточная функция ошибки от регулирующего воздействия  может быть записана по формуле:

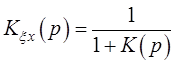                                               (2.1)

Интересной особенностью функции является тот факт, что она представляет собой отношение двух характеристических полиномов: разомкнутой системы  и замкнутой системы . В самом деле, если обозначим передаточную функцию разомкнутой системы в виде

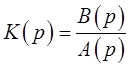                                                (2.2)

то знаменатель этой передаточной функции будет называться характеристическим полиномом разомкнутой системы.

С другой стороны, передаточная функция замкнутой системы тоже имеет свой знаменатель:

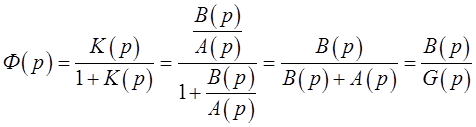                 (2.3)

Полином  называется характеристическим полиномом замкнутой системы.  Теперь, переходя к формуле (2.3), можно записать:

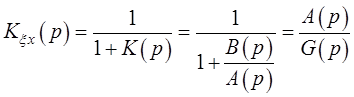                                 (2.4)

что и является отношением двух характеристических полиномов.

Подставим в выражение (2.1) заданную передаточную функцию разомкнутой системы:

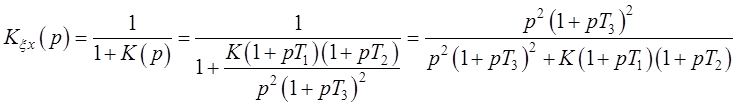   (2.5)

3. Структурная схема исследуемой системы.

Исследуемая система состоит из двух форсирующих, двух инерционных и двух интегрирующих звеньев. Считая систему следящей, необходимо все звенья расположить в канале прямой передачи. С учетом  этого структурная схема имеет следующий вид:

Рис. 3.1. Структурная схема исследуемой системы.

4. Характеристические полиномы разомкнутой и замкнутой системы.

Характеристическим полиномом разомкнутой системы  называется знаменатель передаточной функции разомкнутой системы (см. формулу (2.2)):

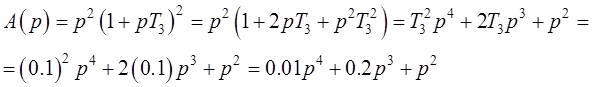                           (4.1)

Характеристическим полиномом замкнутой системы  называется знаменатель передаточной функции замкнутой системы. Этот полином есть не что иное, как сумма полиномов числителя и знаменателя передаточной функции разомкнутой системы (см. формулу (2.3)):

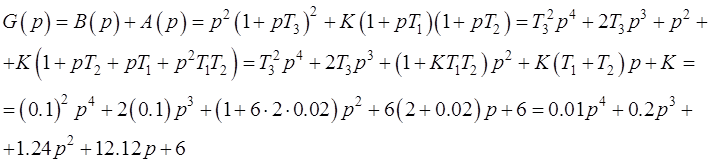      (4.2)

5. Исследование устойчивости системы по критерию Гурвица.

Согласно критерию Гурвица, для того, чтобы система была устойчива, необходимо  наложить определенные условия на коэффициенты характеристического уравнения системы (5.1).

                                          (5.1)

Эти условия можно разделить на необходимые и достаточные. Необходимым условием устойчивости является положительность всех коэффициентов уравнения (5.1):

                                          (5.2)

Если это условие не выполняется, дальнейший анализ можно не проводить – система неустойчива. Если же условие (5.2) выполняется, то проверяется достаточное условие – положительность всех диагональных определителей матрицы Гурвица.

Запишем характеристическое уравнение для заданной системы (уравнение):

                                  (5.3)

Поскольку все коэффициенты характеристического уравнения положительны, то необходимое условие устойчивости Гурвица выполняется.

Для проверки достаточного условия  необходимо сформировать матрицу Гурвица. Для системы с дифференциальным уравнением 4-го порядка характеристическое уравнение будет иметь вид:

                                        (5.4)

а матрица Гурвица выглядит следующим образом:

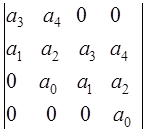                                                  (5.5)

Достаточные условия устойчивости – положительные значения всех диагональных определителей:

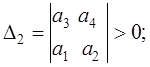
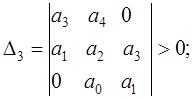
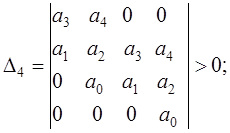         (5.6)

В результате для уравнения 4-степени условия Гурвица сводятся к неравенству:

                                                 (5.7)

Для заданной системы характеристический полином имеет вид (4.2):

Обозначим коэффициенты характеристического полинома:

                     (5.8)

Подставим коэффициенты в неравенство (5.7):

                   (5.9)

Это есть условие устойчивости. Если неравенство превратить в равенство, возникает так называемое критическое состояние системы, когда она находится на грани между устойчивым и неустойчивым состояниями. Коэффициент усиления при этом называют критическим .

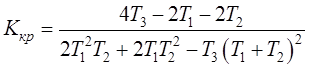                                   (5.10)

Подставим в (5.10) численные значения постоянных времени звеньев:

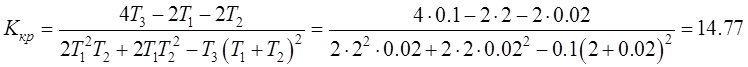
Следовательно, данная система устойчива, т.к. ее коэффициент усиления более чем в два раза меньше критического.

 6. Исследование устойчивости системы по критерию Михайлова методом чередующихся корней.

Запишем характеристический полином заданной системы согласно (4.2):

Перейдем в частотную область:

            (6.1)

Обозначим и вычислим коэффициенты:

     

Найдем частоты пересечения мнимой оси, для чего приравняем к нулю вещественную часть и найдем корни полученного уравнения.

                                 (6.2)

Заменим переменную:

                                              (6.3)