Передаточная функция разомкнутой системы. Характеристические полиномы разомкнутой и замкнутой систем

Министерство Образования Российской Федерации

Новосибирский Государственный Технический Университет

Кафедра РП и РПУ

Вариант - 67

Расчетно-графическое задание по курсу «Радиоавтоматика»

Факультет: РЭФ

Группа: РТ5-04

Студент: Самойлов Е.А.

Преподаватель: Лявданский С.Е.

Новосибирск 2003

Задание:

1.  Записать передаточную функцию разомкнутой системы К(р)

2.  Зарисовать структурную схему системы, считая ее следящей. Перечислить все типовые структурные звенья в системе.

3.  Записать передаточную функцию и дифференциальные уравнения замкнутой системы.

4.  Записать передаточную функцию для ошибки от регулирующего воздействия

5.  Записать характеристические полиномы разомкнутой  и замкнутой систем и  вычислить их коэффициенты.

6.  Произвести анализ устойчивой систем по критерию Гурвица.

7.  Произвести анализ устойчивости системы по критерию Михайлова (метод чередующихся корней). Построить годограф Михайлова.

8.  Произвести анализ устойчивости системы по критерию Найквиста. Построить годограф Найквиста. Определить запас устойчивости системы по модулю и по фазе.

9.  Определить ошибку от регулирования ξ(t) и построить график.

Условие:

Передаточная функция ошибки от регулирующего воздействия:

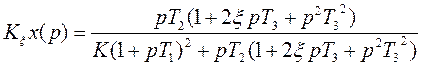
Параметры:

Выполнение:

1. Передаточная функция разомкнутой системы  выражается через передаточную функцию от ошибки регулирующего воздействия, следующим образом:

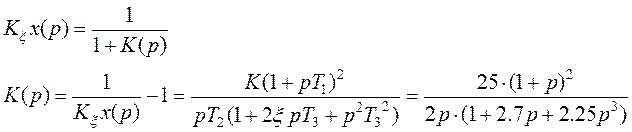
2. На рис.1 изображена структурная схема системы. Двигаясь слева направо, на схеме расположены следующие звенья:

-     Интегрирующее звено

-  Два форсирующих звена

-  Колебательное звено

Рис.1. Структурная схема системы.

3.  Передаточная функция замкнутой системы выражается через передаточную систему разомкнутой системы, следующим соотношением:

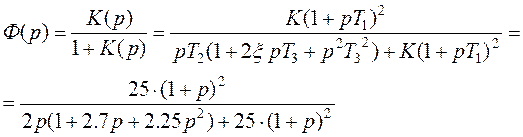
Разложим числитель и знаменатель на множители и составим дифференциальное уравнение:

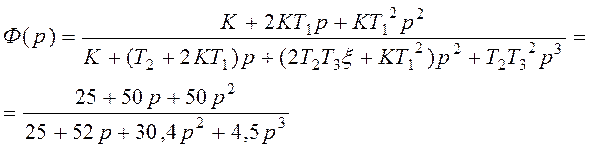
Отсюда дифференциальное уравнение замкнутой системы:

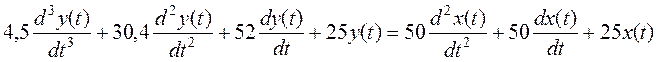
4.  Запишем передаточную функцию для ошибки от регулирующего воздействия.

5. 

Характеристические полиномы разомкнутой и замкнутой систем определяются через передаточную функцию от ошибки регулирующего воздействия.

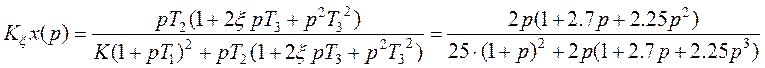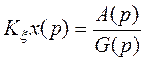 ,   где - характеристический полином разомкнутой системы, а - характеристический полином замкнутой системы.

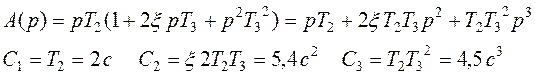
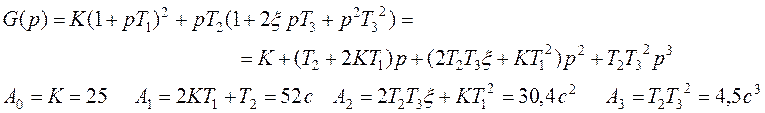
6.  Критерий устойчивости системы по Гурвицу, заключается  в выполнении или невыполнении следующего неравенства.

Если данное неравенство выполняется, то в таком случае система является устойчивой.

Если же неравенство не выполняется, то тогда система является неустойчивой.

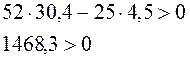
Отсюда следует, что система является устойчивой.

7.  Воспользуемся характеристическим полиномом разомкнутой системы:

Перейдем в частотную область

Найдем частоты пересечения мнимой оси, для чего приравняем к нулю вещественную часть и найдем корни полученного уравнения.

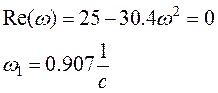
Далее определим частоты пересечения  вещественной оси.

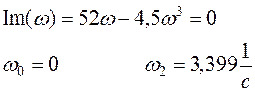
Располагая полученные частоты в ряд, по их возрастанию можно увидеть, что в ряде нет располагающихся друг за другом корней одного и того же уравнения.

Отсюда следует, что кривая годографа не пересекает два раза одну и ту же ось координат. Система устойчива.

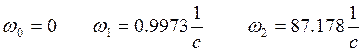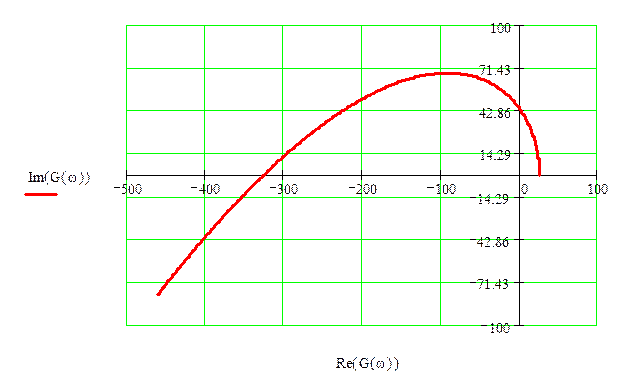
Рис.2. Годограф Михайлова.

Распределение G(ω) при различных значениях ω, показаны в таблице №1

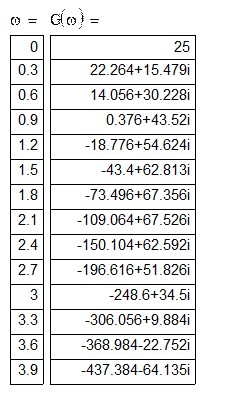8.  Рассмотрим нашу передаточную функцию разомкнутой системы. Имея в наличии четыре последовательных звена проведем их анализ, т.е. посмотрим как ведут себя звенья на разных частотах. На основании этого построим годограф Найквиста.

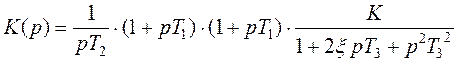
Обозначим

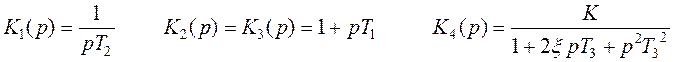
Определим  их модули и аргументы на предельных частотах:

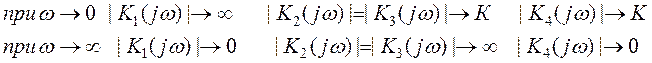
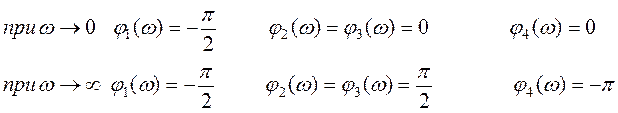
Т.к. звенья соединены последовательно, то можно записать

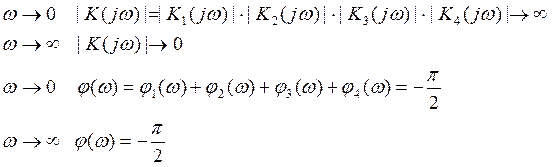
На основании проведенного анализа можно построить годограф Найквиста и таблицу распределения значений передаточной функции разомкнутой системы (Таблица №2).

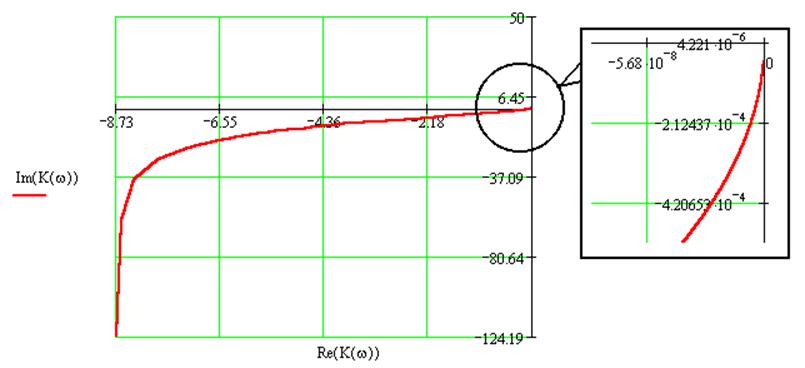
Рис.3.  Годограф Найквиста.

Таблица №2

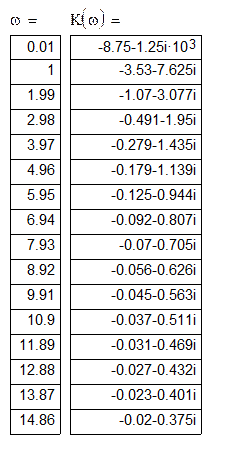Из рис.3 видно, что годограф не охватывает точку (-1; j0), значит система является устойчивой.

Запас устойчивости по модулю определяется по следующей формуле: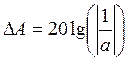 дБ, где а - определяется  по графику на рисунке 4.

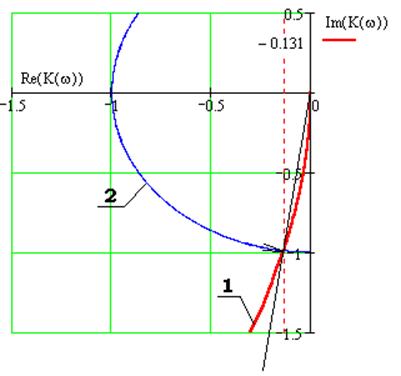
Рис.4. К определению запаса устойчивости по модулю и по фазе: 1- годограф Найквиста, 2 – единичная окружность.

Таким образом получаем, что запас устойчивости по модулю равен:

 

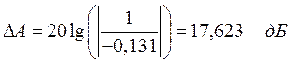
А запас устойчивости по фазе -     

9.  Определим ошибку регулирования ξ(t) методом коэффициентов ошибки.

Разложим передаточную функцию в ряд по степеням комплексной переменной р.

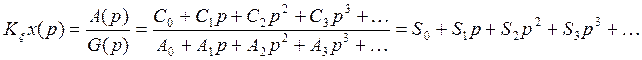
Коэффициенты полинома  называются коэффициентами ошибки. Считая, что порядки характеристических полиномов G(p) и A(p) одинаковы определим коэффициенты ошибки.

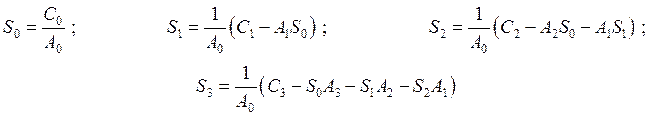
Подставляя значения коэффициентов полиномов, получим искомые величины.

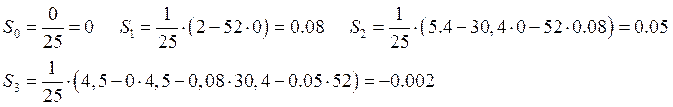Выражение для ошибки регулирования выводится следующим образом

Переходя от опереаторной формы записи дифференциального уравнения к классической, получаем.

Найдем производные заданного сигнала x(t)

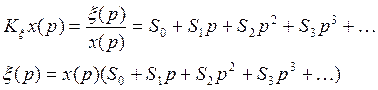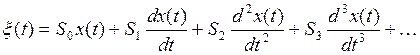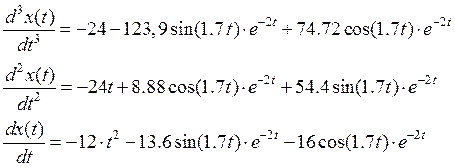
Имея в наличии все слагаемые функции ошибки регулирования, запишем ее и построим ее на координатной плоскости (рис.5).

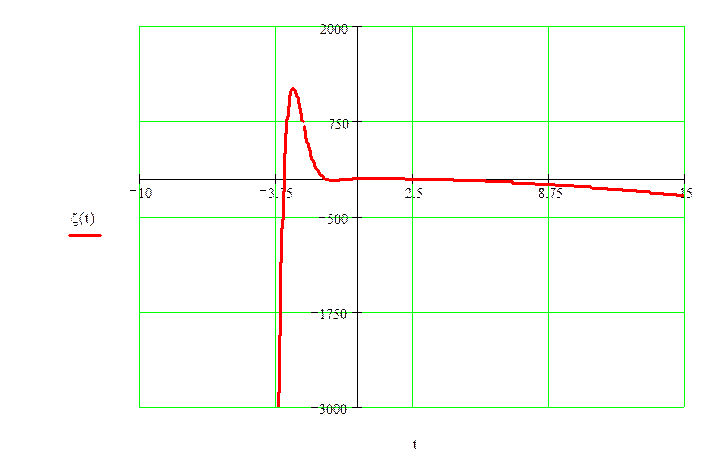Рис.5. Ошибка регулирования.

Список литературы:

1.  С.Е. Лявдаский Методическике пособия по Радиоавтоматике – Новосибирск 1990, 1995 г.г.

2.  И.Г. Коновало Радиоавтоматика – Москва “Высшая школа” 1980 г.

3.  Конспект лекций по Радиоавтоматике