Передаточная функция замкнутой системы. Передаточная функция ошибки от регулирующего воздействия, страница 3

                                                   (10.1)

Запас устойчивости по модулю для заданной системы в дБ: 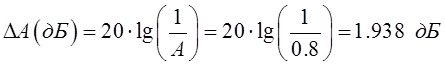                                                                     (10.2)

Запас устойчивости по фазе характеризует удаление годографа от критической точки по дуге окружности единичного радиуса и определяется углом  между отрицательным направлением вещественной полуоси и лучом, проведенным из начала координат в точку пересечения годографа с единичной окружностью.

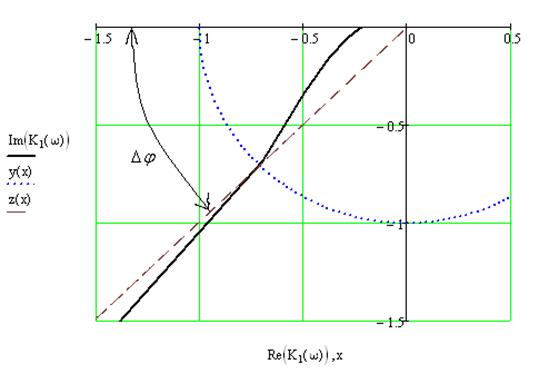
                     Рис. 10.2. Годограф Найквиста с указанием запаса устойчивости по фазе.

Для заданной системы запас устойчивости оказался равным .

 11. Определение ошибки регулирования системы.

Как было показано в пункте 2, передаточная функция ошибки от регулирующего воздействия  является отношением двух характеристических полиномов: разомкнутой и замкнутой системы.

Отношение этих полиномов можно представить в виде некоего третьего полинома, так называемого полинома ошибки с пока что неизвестными коэффициентами:

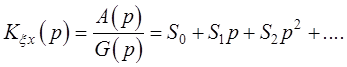                              (11.1)

Коэффициенты полинома  называются коэффициентами ошибки.

Формулу (11.1) можно записать в более удобном виде. Так как передаточная функция есть отношение изображений двух сигналов, то

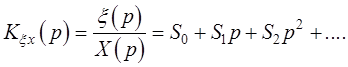                        (11.2)

Записав это в одну строку, получим:

                           (11.3)

или, переходя от операторной (символической) формы записи дифференциального уравнения к классической, получаем:

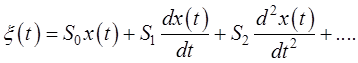                       (11.4)

Таким образом, если определить неизвестные пока коэффициенты ошибки, то искомая ошибка регулирования записывается в аналитической форме через входной сигнал х(t) и его производные.

Самый удобный способ определения коэффициентов ошибки – выразить их через известные коэффициенты характеристических полиномов  и .

Запишем эти полиномы в виде:

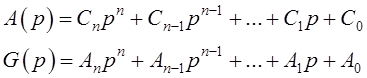                         (11.5)

Возвращаясь к формуле (11.1) и подставляя туда (11.5), путем деления двух полиномов легко найти коэффициенты третьего. В частности,

     

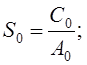
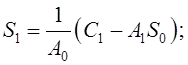
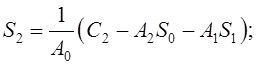
и так далее.

Для заданной системы (2.5):

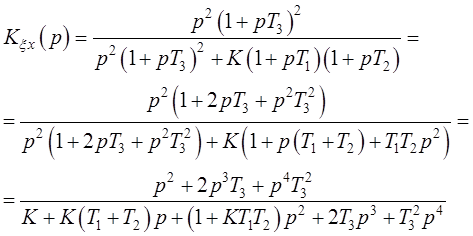                        (11.6)

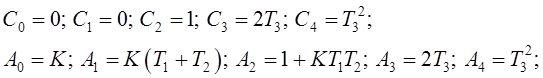
Наличие в системе двух интегрирующих звеньев приводит к равенству нулю коэффициентов  и , а, следовательно, и коэффициентов ошибки  и .

Вычислим коэффициенты  и :

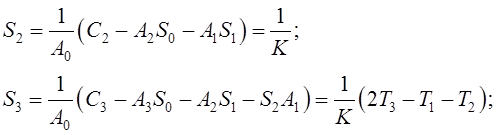              (11.7)

Входное воздействие представлено в виде:

Подставим выражение для входного воздействия в формулу (11.4), учтя при этом равенство нулю коэффициентов ошибки  и , а также всех высших производных, начиная с четвертой:

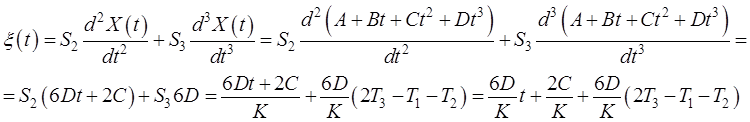 (11.8)

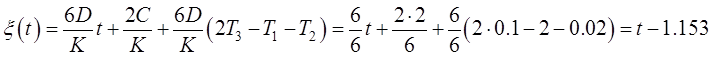    (11.9)

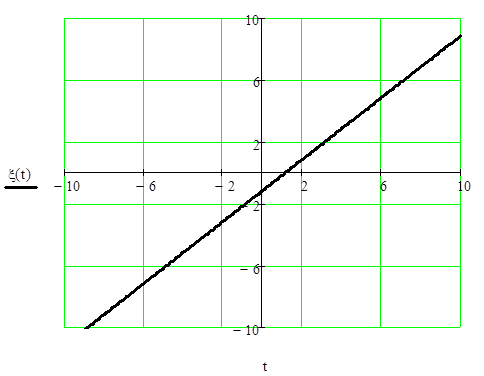                             12. График ошибки регулирования системы.

                                            Рис. 12.1. График ошибки регулирования системы.

СПИСОК ЛИТЕРАТУРЫ

1. Радиоавтоматика. Методические указания к самостоятельной аудиторной работе/сост. Лявданский С.Е. – Новосибирск: Изд–во НГТУ, 1990. – 33 с.  

2. Радиоавтоматика. Методические указания к самостоятельной аудиторной работе/сост. Лявданский С.Е. – Новосибирск: Изд–во НГТУ, 1995. – 35 с.

3. Радиоавтоматика. Под ред. В. А. Бесекерского. – М.: Высш. шк., 1985. – 271 с.