Методические указания по выполнению курсовой работы по курсам "Метрология, стандартизация и технические измерения", "Метрология, стандартизация и сертификация", страница 6

При заданном риске заказчика  β_max должно  выполняться условие в соответствии с (5), (6) и (7):

β (k) +β (m) +  (n – k – m)  β_max = 0, 01, где k – число поверяемых параметров на поверочной установке, m – число параметров, проверяемых на других установках, n – общее число параметров изделия

Если в качестве примера взять из таблицы 4 наилучший (гипотетический) случай β (k = 9)  = 0,0021, тогда допустимый риск   заказчика для  m = 14, β (m = 14) этом для каждого параметра β  0,0005 и класс точности применяемых средств измерений должен быть не хуже 0,01 %.

Рассмотрим пример, когда допуски на каждый проверяемый параметр , т.е. выполняется правило «шести сигм» и случай более точного процесса изготовления, когда в заданный допуск входит «семь сигм» проверяемого параметра. В таблице 5 представлены значения вероятностей брака в зависимости от числа неконтролируемых параметров.

 Таблица 5. Вероятности брака за счёт неконтролируемых параметров

Из таблицы 5 для нашего примера следует, что при отсутствии контроля изделия риск заказчика (вероятность брака при n = 23)  β = 0,011. Это практически соответствует требованиям, но при условии повышения точности технологических процессов изготовления до значений  Из таблицы 5 следует, что повышение точности процессов изготовления позволяет исключать из операций контроля часть параметров, если, например, их по какой-то причине нельзя измерить, либо с целью уменьшения затрат на контроль. При этом ослабляются требования к точности измеряемых параметров. Этот пример ещё раз показывает, что повышение точности технологических процессов является более перспективным направлением вложения средств, нежели бесконечное повышение точности измерений, которое может привести к более значительным затратам, в сравнении с затратами на повышение качества технологических процессов. Использование  функции (9) для расчёта суммарных затрат  на измерительный контроль продукции в реальных условиях организации позволяет проводить эти сравнения при планировании контроля продукции.

1.3 Оптимизация требований к погрешностям измерений по критерию минимума затрат

Определим функцию суммарных затрат на измерения, потери качества измерений и на брак неконтролируемых параметров. В  [2] для приближённых расчётов рекомендована эмпирическая суммарная функция затрат, которая не учитывает допуски на параметры и статистические свойства контролируемых параметров и погрешностей измерения.

В данной работе применим предложенную в [8] модель суммарной функции затрат, которуюпредставим  в следующем виде:

  =(k) +  +  + .            (19)

В данном выражении первое слагаемое определяет затраты на измерения k из n параметров объекта контроля, второе и третье  определяют затраты из-за потерь качества измерений, вследствие ошибок первого и второго рода  и четвёртое определяет потери на брак для (n- ) неконтролируемых параметров. В выражении (19) применены обозначения:

C_Σи (k) – затраты на измерения k параметров одного изделия;

и - коэффициенты затрат (денежные эквиваленты) на потери из-за ошибок первого и второго рода при измерении k из  n пар;

;  и определены формулами (8), (9) и (10);

 – коэффициент затрат на брак по n- k неконтролируемым параметрам по одному изделию.

Затраты на измерения k параметров одного изделия в (19) определяются следующим выражением [8]:

 ,                                                          (20)

где

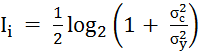,                                                       (21)

– количество информации (в битах), получаемое при измерении i – того параметра для измерительного канала с аддитивным гауссовым шумом [16, 17];