где f (Uci) – априорная плотность вероятности параметра Uci.
Совместная плотность вероятности (5) позволяет определить ошибки первого и второго рода, характеризующие достоверность измерительного контроля многопараметрического объекта.
Средние вероятности ошибок первого и второго рода [4, 6] при контроле i-того параметра определяются с учётом (5) выражениями:
![]() =
= 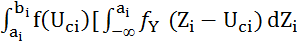 +
+ 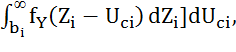 (6)
(6)
![]() =
= 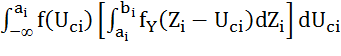 +
+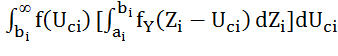 . (7)
. (7)
Здесь: [ ![]() ] – допуск на i-
тый параметр.
] – допуск на i-
тый параметр.
Используя правило сложения для совместимых и взаимно независимых событий [9], получим с учётом (6) и (7) следующие выражения для вероятностей ошибок первого и второго рода для k из n контролируемых параметров:
α
(k) = 1 - ![]() ,
(8)
,
(8)
β
(k) = 1 - ![]() ,
(9)
,
(9)
При этом вероятность брака для (n-k) неконтролируемых параметров равна:
![]() (n - k) = 1-
(n - k) = 1-![]()
![]() (10)
(10)
Здесь:
![]() =
= ![]() +
+ 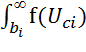 d
d![]() .
(11)
.
(11)
Заметим, что, риск заказчика включает вероятность βi , вычисленную по формуле (9) и вероятность брака (10) по n – k неконтролируемым параметрам.
Из изложенного следует, что для оценки достоверности многопараметрического измерительного контроля при использовании обобщённой модели измерений (1), (2) необходимо определить плотность вероятности f(Yi) суммарной погрешности (3). Это позволяет получить условную плотность вероятности (4) и при заданной априорной плотности вероятности измеряемого параметра f (Uci) определить совместную плотность вероятности (5), которая используется для расчёта средних ошибок первого и второго рода по формулам (6), (7), (8) и (9).
Рассмотрим примеры аппроксимации распределений вероятностей суммарной аддитивной погрешности (3), полезные для практических расчётов.
Пример 1. Для фиксированных случайных значений параметра Uci и систематической погрешности ∆si плотность вероятности суммы (3) в соответствии с правилом свёртки распределений независимых случайных величин [9] определяется выражением:
f
(Yi) = 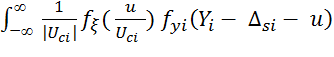 du.
(12)
du.
(12)
Для
гауссовых распределений f
(ξi) и f
(yi) с нулевыми средними и
дисперсиями ![]() плотность вероятности f
(
плотность вероятности f
(![]() ) (12) будет так же гауссовой с
математическим ожиданием µ = Uci
+
) (12) будет так же гауссовой с
математическим ожиданием µ = Uci
+ ![]() и дисперсией:
и дисперсией:
![]() . (13)
. (13)
Тогда условная плотность вероятности (4) примет вид:
p(Zi/Uci)
= 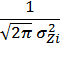 exp
exp 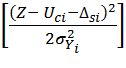 .
(14)
.
(14)
Пример 2. Рассмотрим случай, когда распределения независимых погрешностей в (3) f(ξi) и f(yi) нормальные, а плотность вероятности неисключённой систематической погрешности ∆si – равномерная в интервале [c, d]. Тогда с учётом (12) и (13) получим:
f
(Yi) = ![]()
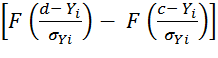 ,
(15)
,
(15)
где F(z) – функция Лапласа [9].
Из выражений (4) и (15) получим условную плотность вероятности:
p(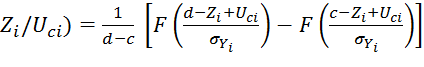 .
(16)
.
(16)
Полученные в приведённых выше примерах 1, 2 выражения (14) и (16) для условных распределений позволяют рассчитать ошибки первого и второго рода (6) и (7) и определить достоверность многопараметрического измерительного контроля (8) и (9) с учётом широко применяемых законов распределения составляющих суммарной погрешности (3).
Пример 3.Представляет
интерес сравнение результатов расчёта ошибок первого и второго рода с
использованием рассмотренного выше математического метода с результатами
имитационного моделирования, приведёнными в [8] для простейшего случая, когда
все параметры одинаковы, а распределение аддитивной погрешности (3) равномерное
в интервале 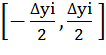 .
.
При нормальном распределении параметров Uci в соответствии с (6) и (7) вероятности ошибок первого и второго рода при симметричном поле допуска для сигнала [ai , bi ] определяются выражениями:
![]() pnorm
pnorm![]() pnorm
pnorm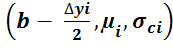 , (17)
, (17)
![]() = pnorm
= pnorm 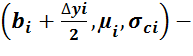
![]()
![]() , (18)
, (18)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.