Методические указания по выполнению курсовой работы по курсам "Метрология, стандартизация и технические измерения", "Метрология, стандартизация и сертификация", страница 4

где pnorm (x, µ, σ) – интегральная функция распределения вероятностей в обозначениях программы Mathcad, µ_i – среднее значение (математическое ожидание) сигнала ,  - СКЗ сигнала, ∆_yi - поле допуска, равномерно распределённой аддитивной погрешности y_i в (3).

Для сравнения с результатами [8], используя выражения (8) и (9) с учётом (17) (18),  рассчитаем вероятности ошибок первого и второго рода α (k) и  β(k) для n – параметрического объекта контроля при числе k измеряемых параметров.

Возьмём исходные данные из [8]:

- число контролируемых параметров k = 15, 30;

-   все параметры одинаковы, допуск на i - тый измеряемый параметр  равен ;

- среднеквадратические значения (СКЗ) сигнала  =  0,8; 0,9; 1,0;

- СКЗ = 0; 0,1; 0,2; 0,3.

Распределение измеряемого параметра - нормальное с нулевым средним и СКЗ равным , распределение погрешности измерения - равномерное в интервале 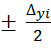. В расчётах используется известное [9] соотношение  .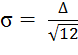

В таблице 1 представлены значения рисков заказчика (R_з) и поставщика (R_п), полученные в работе [8] методом имитационного моделирования для тридцати и пятнадцати контролируемых параметров.

Таблица 1. Результаты моделирования, полученные в [8]

Таблица 2. Результаты расчёта по формулам (8) и (9)

В таблице 2 представлены расчёты ошибок первого и второго рода α(k) и β(k), т.е., рисков поставщика  R_п  и заказчика R_з  соответственно, рассчитанные  по формулам (8) и (9) с учётом (17) и (18). Сравнение данных таблиц 1 и 2 показывает достаточно хорошее совпадение результатов моделирования [5] и приведённых нами расчётов. В таблицах 1,2 выделенные данные при k = 15 учитывают вероятность брака по пятнадцати неконтролируемым параметрам.

Данный пример показывает, что основным недостатком имитационного моделирования является необходимость повтора эксперимента при любых изменениях условий задачи, например, законов распределения измеряемых параметров и погрешностей, допусков на параметры и т.д. Использование этого метода в инженерной практике, тем более в случае обобщённой измерительной модели (1), являются менее эффективными по сравнению с математическими методами расчёта.