



























































1. МЕТОД НАВОДИМЫХ ЭЛЕКТРОДВИЖУЩИХ СИЛ
1.1. ОПИСАНИЕ СВОЙСТВ МНОГОПОЛЮСНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ В ДИАПАЗОНЕ СВЕРХВЫСОКИХ ЧАСТОТ.
Любая
антенная система, содержащая два и более диполей, может рассматриваться как
сверхвысокочастотная (СВЧ) электрическая цепь, имеющая две и более пары зажимов
(полюсов), которыми являются клеммы питания диполей. Иными словами, такая
система, хотя и излучает электромагнитную энергию, является многополюсником
(многоплечим, многопортовым устройством), содержащим совокупность определенным
образом соединенных комплексных сопротивлений. Вещественная часть этих
сопротивлений моделирует (характеризует, описывает) мощность (т.е. активную
энергию в единицу времени), излучаемого диполями и уходящую в безграничное
свободное пространство [far-field(Fraunhofer) region] безвозвратно.
Реактивная же часть этих сопротивлений отражает колебательные процессы обмена
реактивной мощностью между диполями и пространством в непосредственной близости
к диполям (reactivehear-fieldregion). Именно эти,
квазистатические электромагнитные поля, убывающие с
ростом расстояния ![]() по законам
по законам ![]() и
и ![]() ,
обуславливают реактивную составляющую комплексного входного сопротивления любой
антенной системы. Интенсивность именно этих полей должна быть адекватно
оценена, чтобы сначала «обнулить» реактивную составляющую, а уже только потом
согласовать оставшуюся рафинированную («очищенную» от реактивности) активную
составляющую с вещественным внутренним сопротивлением источника сигнала
(транзисторный усилитель, клистрон, магнетрон и т.п.), имеющего коаксиальный
(разъем) или волноводный (фланец) выход. Таким образом, получается, что, в
отличие от классической теории линейных электрических цепей, где источники
имеют либо нулевое (источник ЭДС), либо бесконечно большое (источник тока)
внутренне сопротивление, источники СВЧ энергии характеризуются конечным
внутренним комплексным сопротивлением
,
обуславливают реактивную составляющую комплексного входного сопротивления любой
антенной системы. Интенсивность именно этих полей должна быть адекватно
оценена, чтобы сначала «обнулить» реактивную составляющую, а уже только потом
согласовать оставшуюся рафинированную («очищенную» от реактивности) активную
составляющую с вещественным внутренним сопротивлением источника сигнала
(транзисторный усилитель, клистрон, магнетрон и т.п.), имеющего коаксиальный
(разъем) или волноводный (фланец) выход. Таким образом, получается, что, в
отличие от классической теории линейных электрических цепей, где источники
имеют либо нулевое (источник ЭДС), либо бесконечно большое (источник тока)
внутренне сопротивление, источники СВЧ энергии характеризуются конечным
внутренним комплексным сопротивлением ![]() (аббревиатура
"S" от слова "source" - источник),
причем как правило, используется источник ЭДС
(аббревиатура
"S" от слова "source" - источник),
причем как правило, используется источник ЭДС ![]() .
.
С учетом этих
ограничений рассмотрим произвольную электрическую цепь (рис. 1.1), имеющую
четыре пары полюсов (четыре плеча, порта, коаксиального разъема, волноводных
фланца, входа/выхода; могут быть и другие термины). Сопротивления ![]()
![]() характеризуют внутреннее сопротивление источников
характеризуют внутреннее сопротивление источников ![]() . На
основании второго закона Кирхгофа [1.1, раздел 5.2] запишем уравнения для
контурных токов
. На
основании второго закона Кирхгофа [1.1, раздел 5.2] запишем уравнения для
контурных токов ![]() (следует
отметить, что здесь и далее речь идет о комплексных амплитудах
(следует
отметить, что здесь и далее речь идет о комплексных амплитудах ![]() соответствующих гармонических функций
времени, в обозначениях которых нижний индекс "m " и признак
комплексности (верхняя «точка») с целью сокращения записи опускаются):
соответствующих гармонических функций
времени, в обозначениях которых нижний индекс "m " и признак
комплексности (верхняя «точка») с целью сокращения записи опускаются):
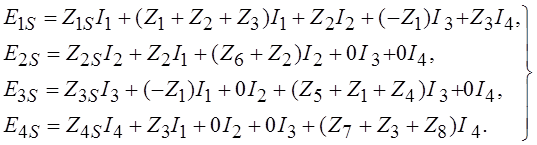 (1.1)
(1.1)
Перенесем
произведение ![]() влево и
обозначим разность
влево и
обозначим разность ![]()
где ![]() фигурирует как «клеммное»
напряжение на зажимах цепи, а «клеммный» ток
фигурирует как «клеммное»
напряжение на зажимах цепи, а «клеммный» ток ![]() - как входной/выходной ток соответствующей пары
полюсов. В результате из уравнений Кирхгофа в терминах контурных токов
рождается система уравнений, связывающих напряжения
- как входной/выходной ток соответствующей пары
полюсов. В результате из уравнений Кирхгофа в терминах контурных токов
рождается система уравнений, связывающих напряжения ![]() с током
с током ![]() на зажимах цепи:
на зажимах цепи:
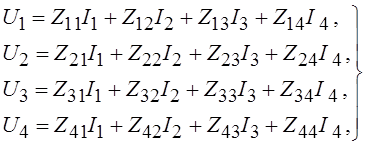 (1.2)
(1.2)
которая может быть записана в матричной форме:
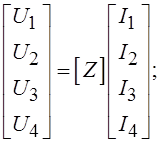
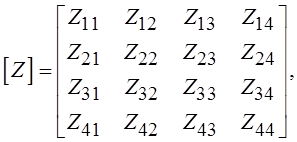 (1.3)
(1.3)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Из первого
уравнения системы (1.2) следует, что собственное сопротивление первого контура ![]() есть отношение напряжения
есть отношение напряжения ![]() на клеммах первого плеча
(порта) к входному току
на клеммах первого плеча
(порта) к входному току ![]() этого
плеча при условии, что токи
этого
плеча при условии, что токи ![]() ,
,
![]() и
и ![]() равны нулю. Это означает, что плечи 2,
3 и 4 разомкнуты (находятся в состоянии холостого хода), а источники сигналов
равны нулю. Это означает, что плечи 2,
3 и 4 разомкнуты (находятся в состоянии холостого хода), а источники сигналов ![]() ,
, ![]() и
и ![]() удалены (отключены):
удалены (отключены):
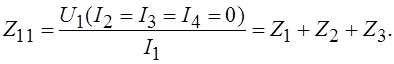 (1.4)
(1.4)
Следует
специально подчеркнуть, что хотя источники ![]() ,
, ![]() и
и ![]() удалены, напряжения на разомкнутых клеммах плеч
2, 3 и 4 могут быть! Эти напряжения обусловлены протеканием тока
удалены, напряжения на разомкнутых клеммах плеч
2, 3 и 4 могут быть! Эти напряжения обусловлены протеканием тока ![]() по сопротивлениям цепи, и с некоторых
из этих сопротивлений напряжения поступают на разомкнутые клеммы оставшихся
плеч 2, 3 и 4. Конкретно для рис.1.1 при возбуждении плеча 1 появится
напряжения на всех оставшихся разомкнутых плечах 2, 3 и 4, так как взаимные
сопротивления
по сопротивлениям цепи, и с некоторых
из этих сопротивлений напряжения поступают на разомкнутые клеммы оставшихся
плеч 2, 3 и 4. Конкретно для рис.1.1 при возбуждении плеча 1 появится
напряжения на всех оставшихся разомкнутых плечах 2, 3 и 4, так как взаимные
сопротивления ![]() ,
, ![]() и
и ![]() отмечены от нуля. В тоже время при возбуждении
плеча 2 появиться напряжение только на разомкнутых клеммах плеча 1 (т.к.
отмечены от нуля. В тоже время при возбуждении
плеча 2 появиться напряжение только на разомкнутых клеммах плеча 1 (т.к.![]() ), а на разомкнутых
клеммах плеч 3 и 4 напряжение не появиться (т.к.
), а на разомкнутых
клеммах плеч 3 и 4 напряжение не появиться (т.к. ![]() ,
, ![]() ).
).
По аналогии с (1.4) определяются оставшиеся собственные сопротивления:
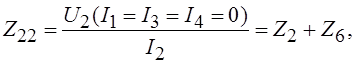 (1.5)
(1.5)
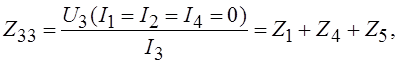 (1.6)
(1.6)
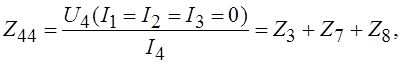 (1.7)
(1.7)
Аналогично из
первого уравнения системы (1.2) определяется взаимное сопротивление ![]() :
:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.