Пример 8. Рассчитать посадку ступицы на цилиндрический вал с d = 50 мм, d1 = 0, d2= 70 мм, l = 80 мм. Материал деталей – сталь (Е = 21,5·104 МПа, m = 0,3). Крутящий момент Т = 240 Н×м; осевая нагрузка Fa = 800 Н. Сборка тепловая.
Решение. Коэффициенты – формула (35):
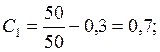
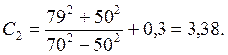
Коэффициент трения f= 0,13 (табл. 10); коэффициент запаса К = 1,5; расчётный натяг – формула (36):
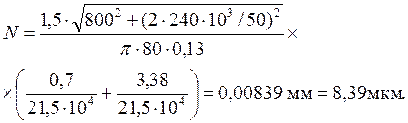
Принимаем предварительно посадку
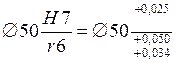
с минимальным табличным натягом Nmin = 0,034 – 0,025 = 0,009 мм = 9 мкм > N. Далее проверяем пригодность более лёгкой и дешёвой посадки при вероятности неразрушения Р < 1.
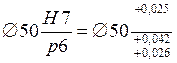с Nmin = 26 – 25 = 1 мкм.
 |
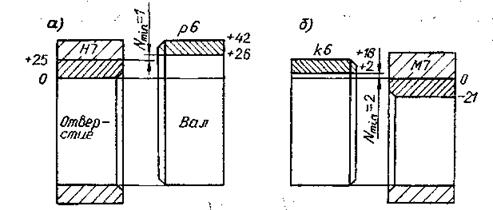Рис. 29. Поля допусков посадок с натягом
Поля допусков новой посадки представлен на рис. 29, а. Основное отклонение вала ei= 26 мкм. Допуски вала и отверстия ITd = IT6 = 42 – 26 = 16 мкм, ITD= IT7 = 25 мкм. Средний натяг Nm = 26 + 0,5×(16 – 25) = 21,5 мкм. Среднее квадратичное отклонение табличного натяга – формулы (43, 44):
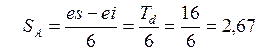мкм; 
мкм;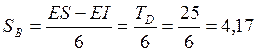
мкм.
Квантиль нормального распределения uP = 2,33 при Р = 0,99 (табл. 11). Минимальный вероятностный натяг NPmin= 21,5 – 2,33×4,95 = 10 мкм.
Вывод. Окончательно принимаем посадку 
при вероятности неразрушения Р =
0,99. Аналогичный выбор можно сделать по таблице вероятностных натягов (табл. 12).
Пример 9. По исходным данным и решению примера 8 рассчитать посадку при механической сборке. Расчётный натяг N = 8,39 мкм. Rz1 и Rz2 – Максимальные высоты микронеровностей Rz1 = 6,3 мкм, Rz2 = 10 мкм.
Решение. Поправка на шабровку:
мкм.
Технологический
натяг 
мкм.
По табл. 12 принята посадка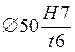 
с Nmin = 29 мкм > 28 при вероятности Р
=1, что подтверждается расчётом натяга по предельным отклонениям: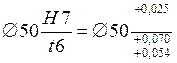 
; Nmin =54 – 25 = 29мкм.
Также
из табл. 12 принята посадка 
с Nрmin = 30 мкм при вероятности Р =
0,95 (без расчёта).
Вывод. При механической сборке принята посадка Æ50Н7/s6 с вероятностью Р = 0,95.
Пример 10. По исходным данным и решению примера 8 рассчитать посадку в системе вала по вероятности неразрушения с основным отклонением Æ50k6. Расчётный натяг N = 8,39 мкм. Сборка тепловая.
Решение. Проверяем посадку:
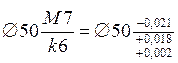с Nmin = 2 мкм (рис. 29, б).
Рассчитан вероятностный натяг при вероятности Р = 0,99. Квантиль нормального распределения uP = 2,33 (табл. 11). Допуски вала ITd= IT6 = 18 – 2 = 16 мкм, отверстия ITD = IT7 = 21 мкм; средний натяг
мм.
Среднее квадратичное отклонение табличного натяга:
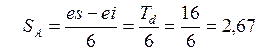мкм; 
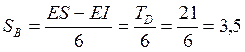мкм;
мкм.
Минимальный вероятностный натяг NPmin= 20,5 – 2,33×4,4 = 10 мкм. Это больше расчётного натяга.
Вывод. В системе вала принимаем посадку Æ50M7/k6 с вероятностью Р = 0,99.
Пример 10. Пересчитать на систему вала с
основным отклонением Æ50k6 посадку
Æ50H7/d11 (рис. 30, а).
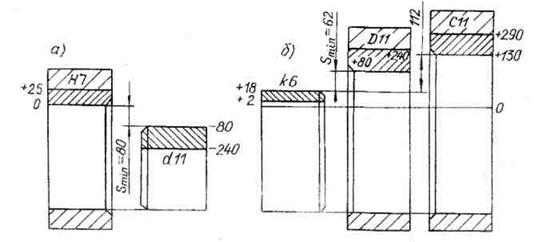
Рис. 30. Поля допусков посадок с зазором
Решение. Предельные отклонения размеров (табл. 9):
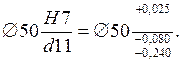
Минимальный зазор Smin= 80 мкм.
Предварительно
принята посадка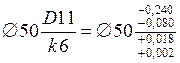 
(рис. 30, б). Она даёт минимальный зазор Smin = 80 – 18 = 62 мкм < 80 мкм, что
недостаточно. Принимаем посадку с большим зазором
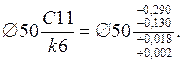
Минимальный зазор Smin = 130 – 18 = 112 мкм > 80 мкм.
Вывод. В системе вала принимаем посадку
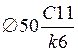вместо посадки 
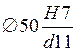в
системе отверстия.
Пример
11. По исходным данным и решению примера 8 рассчитать давление в
соединении с посадкой Æ50H7/r6. Номинальный диаметр d = 50 мм, минимальный натяг Nmin = 9 мкм, коэффициенты 
модуль упругости Е = 21,5·104 МПа.
Решение. Предельные отклонения размеров (табл. 9):
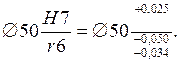
Давление в соединении – формула (34):
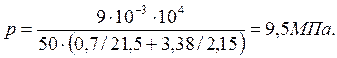
5.3. Посадки подшипников качения
Выбор посадок зависит от вида нагружения колец, действующих нагрузок, режима работы и условий эксплуатации. Различают три случая нагружения колец подшипников:
1) местное, когда кольцо неподвижно относительно радиальной нагрузки;
2) циркуляционное, когда кольцо вращается относительно радиальной нагрузки;
3) колебательное.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.