Исследование математической модели «Гонка вооружений между двумя странами»

Описание модели

Для упрощения задачи были сделаны некоторые предположения, облегчающие процесс моделирования.

Предположение:

Примем, что общее количество вооружений у каждой страны изменяется со временем в зависимости от следующих факторов:

-  Количество оружия у противника

-  Износ собственного вооружения

-  Степень недоверия между противниками

Таким образом мы имеем два уравнения, характеризующих темпы прироста и уменьшения вооружения под влиянием вышеперечисленных факторов:

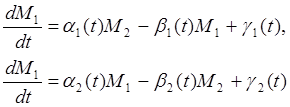                                                              (1)

В уравнение (1) M₁(t)³0, M₂(t)³0 – объем вооружений, коэффициенты a₁>0, a₂>0, b₁>0, b₂>0 характеризуют скорость «старения» вооружений (аналог процесса амортизации производственных мощностей в моделях экономики), функции g₁(t)³0, g₁(t)³0 описывают уровень взаимной настороженности (недоверия) конкурентов, который считается не зависящим от количества вооружений, а определяется другими величинами.

Также следует заметить, что эта модель дает возможность проанализировать ряд важных свойств данного процесса, но не позволяет учесть многих важных факторов, влияющих на динамику процесса. Задачу можно ещё упростить, рассмотрев более частный случай, когда α, β, γ являются константами:

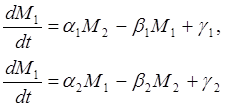                                                                         (2)

Система находится в равновесном состоянии при =0 и =0. Тогда:

α₁M₂-β₁M₁+γ₁=0

α₂M₁-β₂M₂+γ₂=0

Решение:

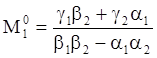
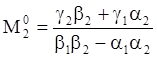                                                                                       (3)

Для существования равновесия при положительных М₁ и М₂ необходимо выполнение неравенства:

β₁β₂ > α₁α₂                                                                                                     (4)

Смысл условия (4) проясняется из следующих рассуждений. Пусть, например, параметры a₁, b₁, b₂ неизменны, а параметр a₂ увеличивается. Это означает, что первая страна не меняет свою стратегию в области вооружений, а вторая наращивает вооружения при неизменном темпе износа оружия (параметр b₂). Тогда при достаточно большой величине a₂ равновесие станет заведомо невозможным, а неравенство (4) обязательно нарушиться. Заметим, что если оба параметра g₁, g₂, характеризующие взаимное недоверие, равны нулю, то положение равновесия отвечает отсутствие вооружений у обеих сторон.

Изучив теперь вопрос об устойчивости равновесия (3) при условие (4). В этом случае интегральные уравнения (2) в плоскости M₁, M₂ имеют вид:

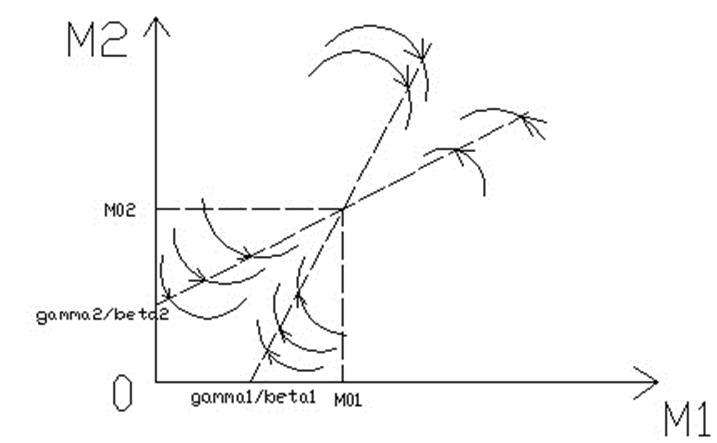
Штриховые прямые отвечают изоклинам нуля (M₂ = a₂/b_2*M₁+g₂/b₂) и бесконечности (M₂ = a₁/b_1*M₁+g₁/b₁). Изоклин нуля имеет наклон, меньший, чем изоклин бесконечности (это следует из неравенства (4)). Сплошным линиям соответствуют интегральные кривые. Стрелками показано направление движения по интегральным кривым с течением времени. Функции M₁(t) и M₂(t) при возрастание t стремятся к равновесным значениям. Таким образом, равновесие устойчиво: любое отклонение от него становиться ничтожно малым по прошествии достаточно большого промежутка времени.

Исследование модели

Замечание 1: Исследование проводилось с использование программного пакета Maple 5

Для исследования предложены следующие варианты:

1.  a1(t) = 0.1, a2(t) = 0.2, b1(t) =0.3, b1(t) =0.1,g1(t) = 10, g2(t) = 20 M1(0)=1000, M2(0)=500, t=0…10

2.  a) g1(t) = 10*|sin(t)|                b) g1(t) = 10*|sin(t/2)|

3.  a) g2(t) = 5*|cos(t)|                 b) g2(t) = 5*|cos(2*t)|

4.  a1(t) = 0.3, a2(t) = 0.1, b1(t) = 0.2, b2(t) = 0.1

Замечание 2: Шаг у всех численных решений 0,4

1)  Первый случай не один из показателей не зависит от времени. Аналитическое решение имеет следующий вид:

m1 := 638.6751346*exp(-.3732050808*t)+61.32486555*exp(-.2679491924e-1*t)+299.9999999+.1000000000e-6*exp(-.3464101616*t)+.500000000e-8*exp(.3464101616*t)

m2 := 167.5426479*exp(-.2679491924e-1*t)-467.5426480*exp(-.3732050808*t)+.900000000e-8*exp(.3464101616*t)+799.9999999+.1000000000e-6*exp(-.3464101616*t)

Соответственно графики:

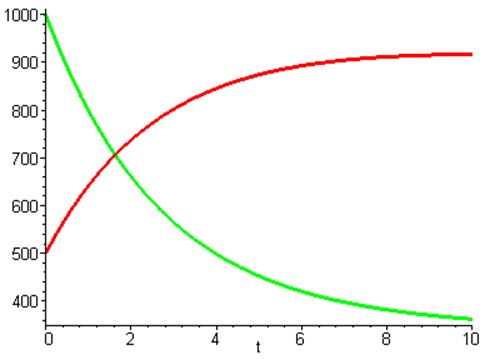
Как видно из графика первая страна проигрывает в гонке. Объясняется это тем что износ оружия больше чем прирост, кроме того уровень недоверия ниже чем у второй страны, соответственно и скорость наращения количества оружия будет меньше. Не смотря на то что вторая страна начинает гонку с 500 ед. , она выигрывает. Вообщем из – за того что уровень износа ниже чем прироста и уровень недоверия выше чем у первой страны, что обеспечивает большую скорость наращивания вооружения.

Численное решение:

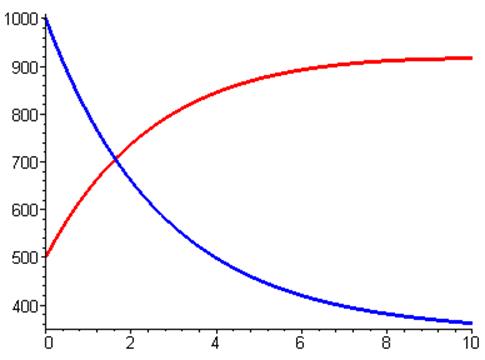
Зависимость M2 от M1:

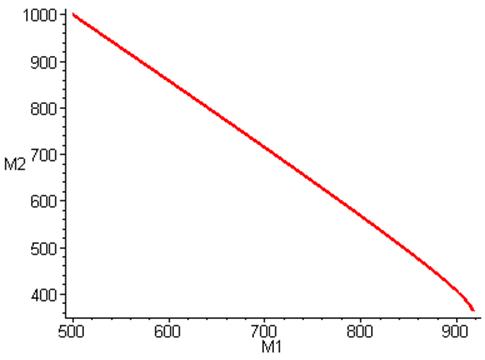
Данном случае аналитическое решение совпадает с численным.

2)  В этом случае экспериментируем со степенью недоверия первой страны к второй, присваивая ей значения меняющиеся со временем.

a) Аналитическое решение:

M1(t) := 200.0000000-(-666.7301839*exp(-.3732050808*t)*sin(t)-142.3041115*exp(-.2679491924e-1*t)*sin(t)+9.034295237*abs(sin(t))*cos(t)-2.640119288*abs(sin(t))*sin(t)+.2000000000e-8*abs(sin(t))*cos(t)*exp(-.3464101616*t)-.4000000000e-10*abs(sin(t))*sin(t)*exp(-.3464101616*t)+.2000000000e-8*abs(sin(t))*cos(t)*exp(.3464101616*t)-.4000000000e-9*abs(sin(t))*sin(t)*exp(.3464101616*t))/sin(t)

M2(t) := 600.0000000+(388.7820620*exp(-.2679491924e-1*t)*sin(t)-488.0803693*exp(-.3732050808*t)*sin(t)-.9999999999e-9*abs(sin(t))*cos(t)*exp(.3464101616*t)-.7016928329*abs(sin(t))*cos(t)-1.736689764*abs(sin(t))*sin(t)+.9999999999e-8*sin(t)*exp(.3464101616*t)+.9999999999e-7*sin(t)*exp(-.3464101616*t))/sin(t)

Графики соответствующие решению:

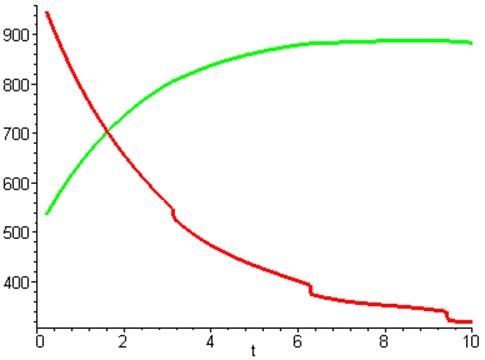Собственно графики очень похожи на первый случай, особенно общая тенденция – уменьшения оружия у первой страны и увеличения у второй.

Недоверие первой страны изменяется по гармоническому закону. Но амплитуда по-прежнему меньше чем у второй страны, а следовательно уменьшение неминуемо. Первая страна опять проигрывает, не смотря на начальный потенциал в 2 раза больший чем у второй страны.