Неравномерность изменения количества оружия у первой страны обусловлена гармоническим законом изменения недоверия первой страны.
Численное решение:
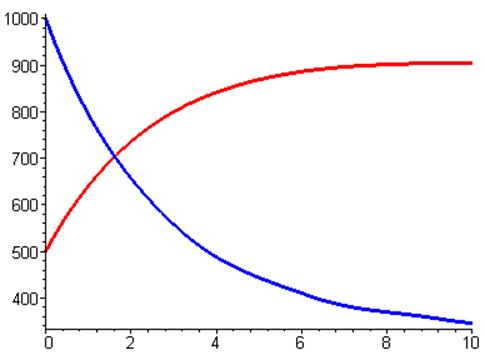
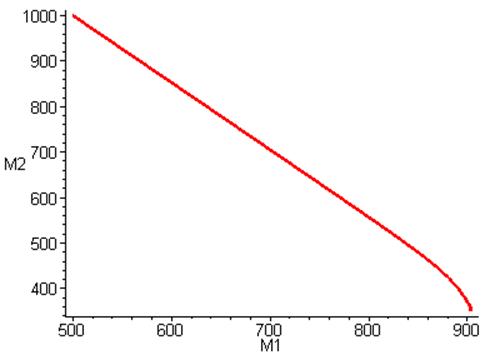
Зависимость M2 от M1:
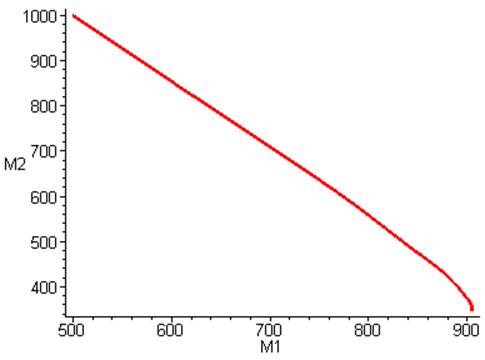
b) Аналитическое решение:
m1 := 200.0000000-(-669.9374893*exp(-.3732050808*t)*sin(.5000000000*t)-144.4067730*exp(-.2679491924e-1*t)*sin(.5000000000*t)+14.34426229*abs(sin(.5000000000*t))*cos(.5000000000*t)-7.786885244*abs(sin(.5000000000*t))*sin(.5000000000*t)+.2000000000e-8*abs(sin(.5000000000*t))*cos(.5000000000*t)*exp(-.3464101616*t)-.2000000000e-9*abs(sin(.5000000000*t))*sin(.5000000000*t)*exp(-.3464101616*t)+.2000000000e-8*abs(sin(.5000000000*t))*cos(.5000000000*t)*exp(.3464101616*t)-.9999999999e-9*abs(sin(.5000000000*t))*sin(.5000000000*t)*exp(.3464101616*t))/sin(.5000000000*t)
m2 := 600.0000000+(394.5266405*exp(-.2679491924e-1*t)*sin(.5000000000*t)-490.4282799*exp(-.3732050808*t)*sin(.5000000000*t)-4.098360660*abs(sin(.5000000000*t))*cos(.5000000000*t)-4.918032787*abs(sin(.5000000000*t))*sin(.5000000000*t)+.9999999999e-8*sin(.5000000000*t)*exp(.3464101616*t)-.9999999999e-9*abs(sin(.5000000000*t))*cos(.5000000000*t)*exp(-.3464101616*t)+.9999999999e-7*sin(.5000000000*t)*exp(-.3464101616*t))/sin(.5000000000*t)
Соответственно графики:
Опять же общая тенденция не изменилась. Хотя на
графике второй страны появились неравномерности, обусловленные соответственно
законом изменения вооружения первой страны. А у первой страны недоверие
изменяется по синусоидальному закону в двое меньшей частой.
Собственно почему произошло незначительное но падение у второй страны. Все произошло из-за того что прирост вооружения второй страны в нашей модели связан с количеством вооружения у первой.
Численное решение:
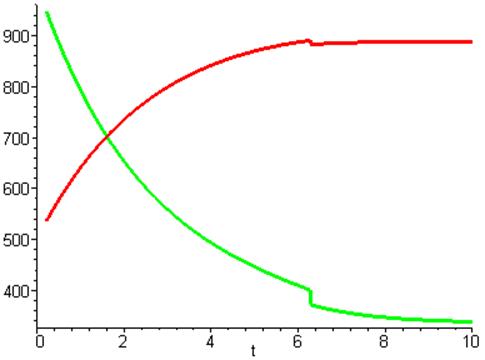
M2 от M1
3) Теперь недоверие первой страны ко второй будем изменять во времени.
a) Аналитическое решение:
m1 := 99.99999997+(276.7562719*exp(-.2679491924e-1*t)*cos(t)+623.6779005*exp(-.3732050808*t)*cos(t)-.1000000000e-10*abs(cos(t))*cos(t)*exp(.3464101616*t)-.4341724412*abs(cos(t))*cos(t)+.1754232080*abs(cos(t))*sin(t)+.6000000000e-8*cos(t)*exp(.3464101616*t)+.2000000000e-10*abs(cos(t))*cos(t)*exp(-.3464101616*t)+.1000000000e-8*abs(cos(t))*sin(t)*exp(-.3464101616*t)+.6000000000e-7*cos(t)*exp(-.3464101616*t))/cos(t)
m2 := 200.0000000+(-456.5639104*exp(-.3732050808*t)*cos(t)+756.1121956*exp(-.2679491924e-1*t)*cos(t)+.4517147619*abs(cos(t))*cos(t)+4.867994037*abs(cos(t))*sin(t)+.2000000000e-10*abs(cos(t))*cos(t)*exp(-.3464101616*t)+.3000000000e-9*abs(cos(t))*sin(t)*exp(-.3464101616*t)+.9999999999e-8*cos(t)*exp(-.3464101616*t)+.2000000000e-9*abs(cos(t))*cos(t)*exp(.3464101616*t)+.6999999999e-9*abs(cos(t))*sin(t)*exp(.3464101616*t))/cos(t)
Графики решений:
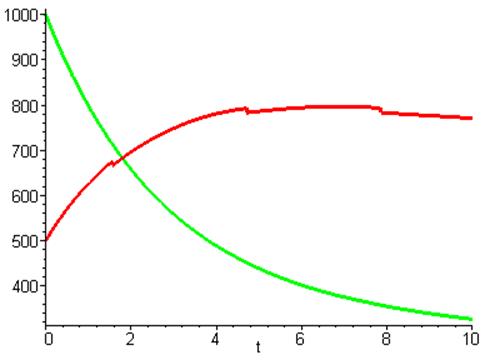Недоверие у второй страны теперь изменяется по
косинусоидальному закону с амплитудой меньшей чем у первой страны. Но между тем
вторая страны выигрывает опять, хотя из графика видно что со временем она
начинает терять свой потенциал, так как недоверие периодически становиться
равным нулю, что притормаживает наращивание потенциала.
Численное решение:
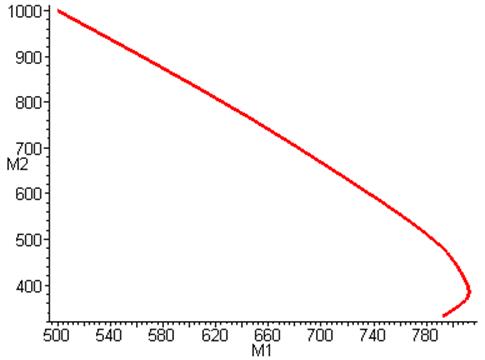
M2 от M1
b) Аналитическое решение:
m1 := 99.99999997-(-623.3352181*exp(-.3732050808*t)*cos(2.*t)-276.7852522*exp(-.2679491924e-1*t)*cos(2.*t)-.6000000001e-7*cos(2.*t)*exp(-.3464101616*t)+.9999999999e-12*abs(cos(2.*t))*cos(2.*t)*exp(-.3464101616*t)+.1204702870*abs(cos(2.*t))*cos(2.*t)-.2415444340e-1*abs(cos(2.*t))*sin(2.*t)-.6000000001e-8*cos(2.*t)*exp(.3464101616*t)-.9999999999e-10*abs(cos(2.*t))*sin(2.*t)*exp(.3464101616*t))/cos(2.*t)
m2 := 200.0000000+(756.1913717*exp(-.2679491924e-1*t)*cos(2.*t)-456.3130496*exp(-.3732050808*t)*cos(2.*t)+.1216780092*abs(cos(2.*t))*cos(2.*t)+2.481869073*abs(cos(2.*t))*sin(2.*t)+.7999999999e-10*abs(cos(2.*t))*cos(2.*t)*exp(.3464101616*t)+.5000000001e-9*abs(cos(2.*t))*sin(2.*t)*exp(.3464101616*t)+.1000000000e-7*cos(2.*t)*exp(-.3464101616*t)+.6000000000e-11*abs(cos(2.*t))*cos(2.*t)*exp(-.3464101616*t)+.3999999999e-9*abs(cos(2.*t))*sin(2.*t)*exp(-.3464101616*t))/cos(2.*t)
Графики:
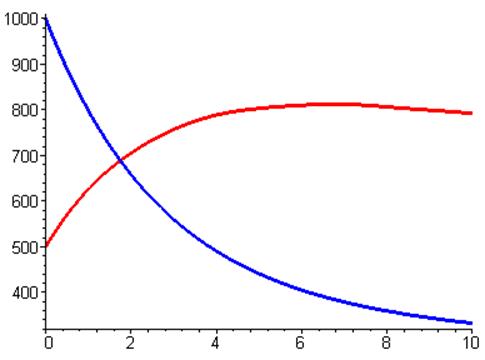
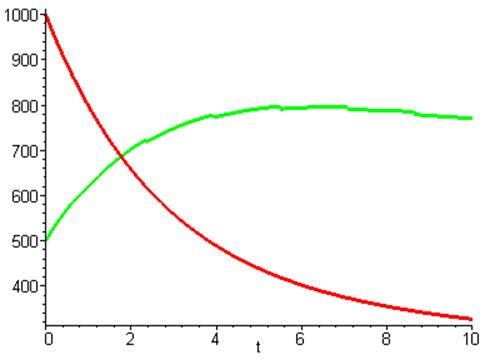Тенденция в графиках не
изменилась, опять лидирует вторая страна. Теперь в отличие от случая а) вторая
страна не смогла создать больший потенциал (судя по графикам). Объяснятся тем
что амплитуда недоверия сравнительно мала, а частота в два раза больше, т.е.
страна позволяла себе «расслабится» чаше чем в случае а).
Численное решение:
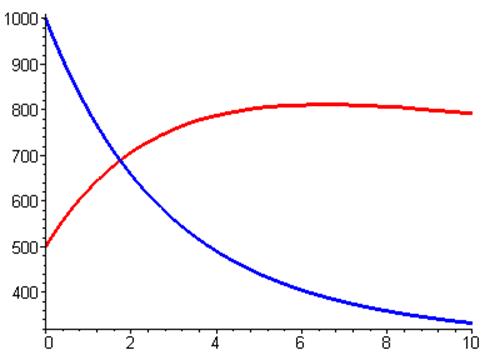
M2 от M1:
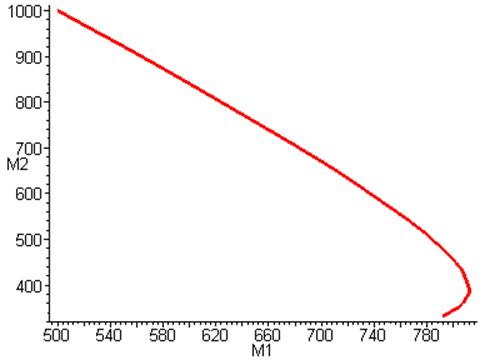
4) Вернемся к тому что все показатели развития не зависят от времени и немного их изменим.
Аналитическое решение:
m1 := 1446.302711*exp(.3027756377e-1*t)+253.6972883*exp(-.3302775638*t)-.1000000000e-7*exp(.3605551276*t)-700.0000001-.1000000000e-6*exp(-.3605551276*t)
m2 := -110.1702158*exp(-.3302775638*t)+1110.170216*exp(.3027756377e-1*t)-500.0000000-.600000000e-8*exp(.3605551276*t)
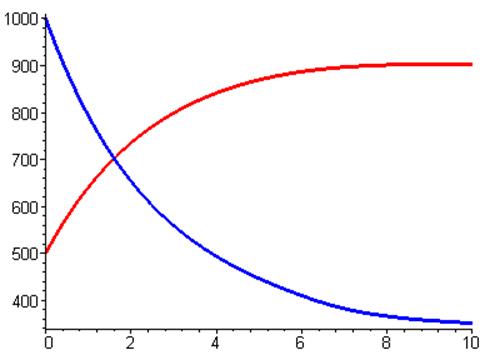
Графики:
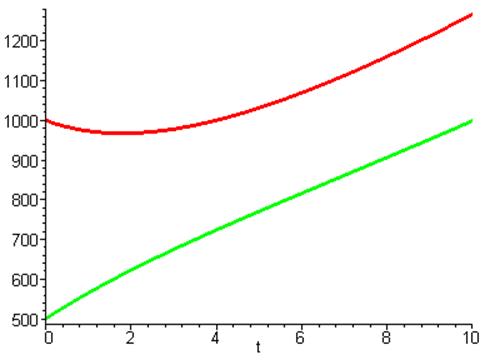Теперь ситуация изменилась:
Выигрывает на этот раз первая страна, но вторая сохраняет тенденции развития,
хотя недостаточного для опережения первой.
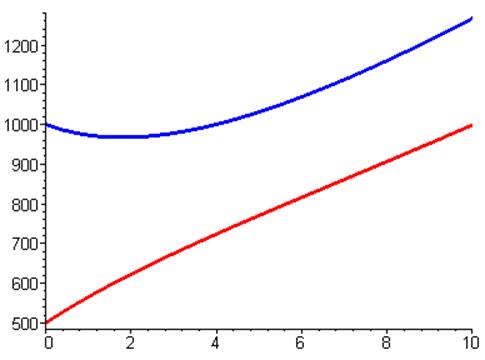
Небольшой спад в начале у первой страны вызван значительным износом оружия и степенью недоверия, которая меньше чем у второй страны. Но тем не менее у первой страны теперь работает лучше производство и ее прирост оружия больше чем износ и поэтому страна начинает наращивать вооружение.
Вторая страна имеет в равной степени износ и прирост оружия и все таки она продолжает наращивать вооружение. Обусловлено это сравнительно большей степенью недоверия к первой стране. Процесс наращивания идет практически линейно.
Численное решение:
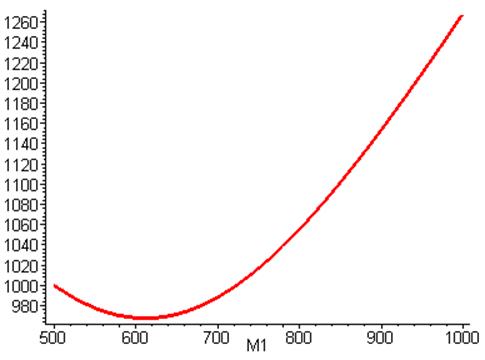
M2 от M1:
Выводы: В результате проделанной работы была исследована математическая модель «Гонка вооружений между двумя странами». Были проведены опыты с изменением параметров модели. Полученные результаты соотносятся с логическими ожиданиями процесса. Так же выявлено, что в гонке вооружений не маловажную функцию играет степень недоверия к противнику. Это можно пронаблюдать на последнем, 4 эксперименте, когда износ и прирост второй страны равны (т.е. компенсируют себя) и между тем идет наращивание оружия.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.