Написание программы, описывающей колебания мембраны

Лабораторная работа №3

Уравнение колебания мембраны

Цель: написать программу, описывающую колебания мембраны

Уравнение колебаний мембраны выглядит следующем образом:

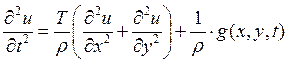
Для простоты решения предположим, что на мембрану не действуют внешние силы, т.е

Уравнение колебания круглой мембраны получим, перейдя  в сферические координаты:

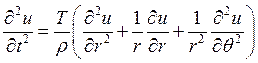
где      T – сила натяжения,

p – плотность мембраны

Начальные условия:

 начальная форма мембраны

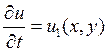
 на  границе = 0

Разностная схема аппроксимирующее дифференциальное уравнение:   

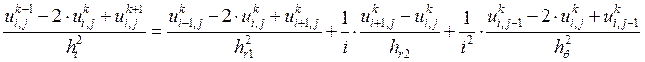         (1)

начальная форма мембраны:

Условие 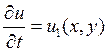 преобразуем к виду (учтя, что =0): 

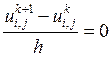
откуда

Пусть сила натяжения и плотность мембраны равны 1. Шаги по осям x, y, t возьмем одинаковые.

Подставим условие  в уравнение (1) и выразим  получим:

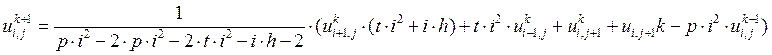
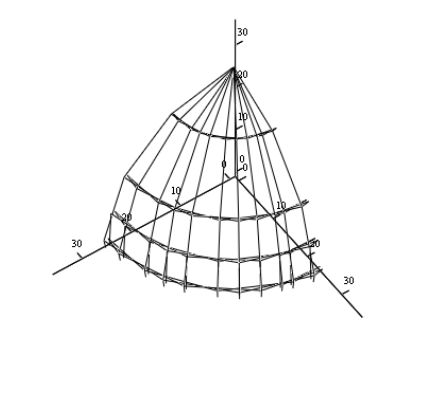
Составляя программу, получим следующие результаты:

При t =0:

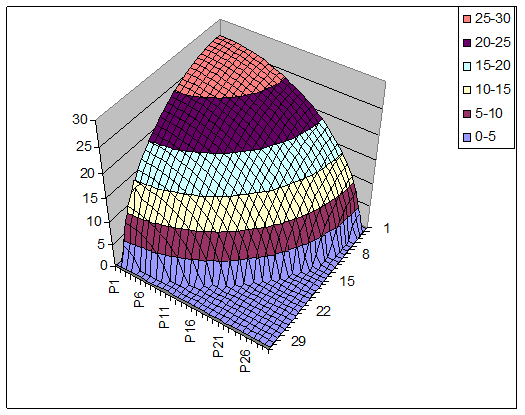
при t=5

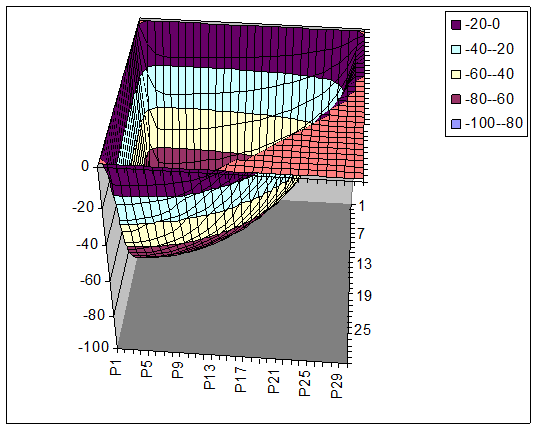
при t = 20:

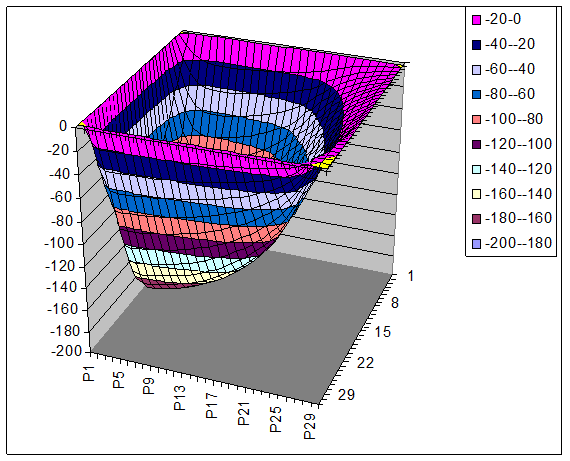
при t =25

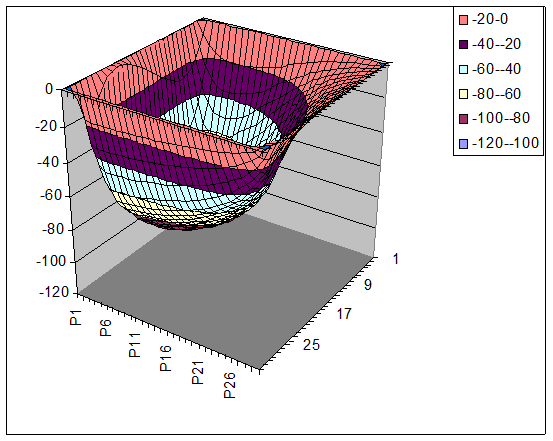
Вывод: В ходе работы была написана программа, описывающая уравнение колебания мембраны. Для нахождения алгоритма построения было найдено численное решение при помощи составления разностной сетки.