Цель работы: Исследование явления переноса.
Задание: Решить систему дифференциальных уравнений, описывающих распределение температуры и поле скорости движения жидкости.
Графическая постановка задачи:
|
|
|
|
|
|
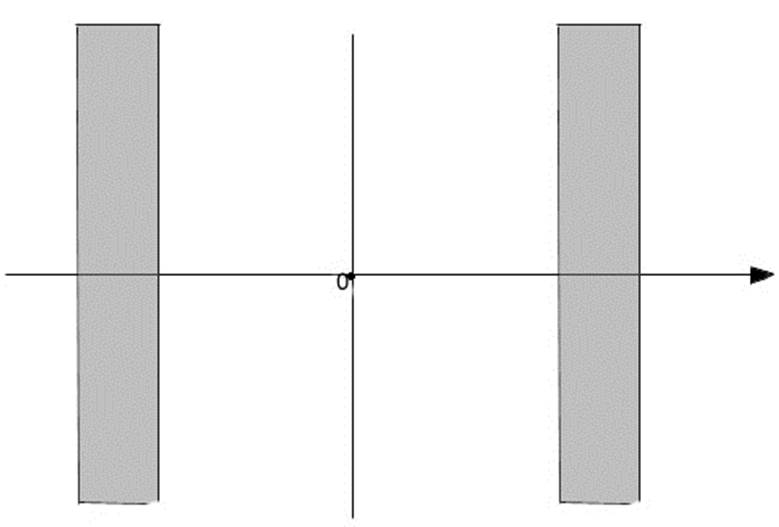
Математическая постановка задачи для температуры:
![]()
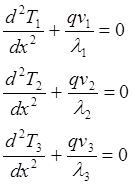 (1)
(1)
Граничные условия:
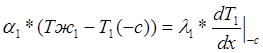
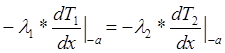
![]() (2)
(2)
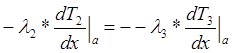
![]()
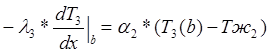
Математическая постановка задачи для поля скорости:
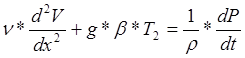 (3)
(3)
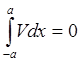 граничные условия: V(±a)=0 (4)
граничные условия: V(±a)=0 (4)
Решение:
Прежде всего найдем выражения для каждой из температур, в соответствии с заданными fi(x) = (sin(x), cos(x), ln(x)):
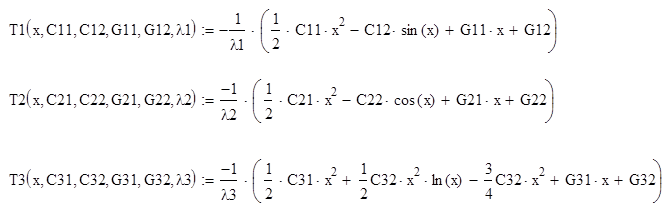
Соответственно производные:
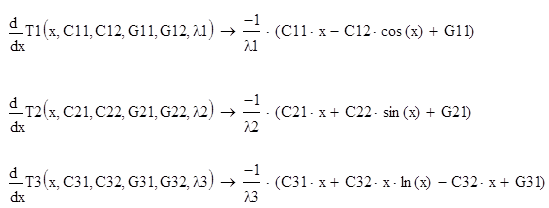
Теперь найдем интересующие нас коэффициенты, а т.е. C21, C22, ведь нам нужно узнать как ведет себя температура и поле скорости в канале (-а до а). Пользуясь граничными условиями (2) для температур, находим коэффициенты. Решение задачи удобнее всего производить пользуясь программным комплексом Maple версии 5 или 6. Из-за большого размера найденных коэффициентов, в отчете они не отображаются, пронаблюдать их можно в листинге программы.
Теперь найдем выражение для скорости:

Чтобы найти неизвестные коэффициенты, появившиеся при интегрирование, воспользуемся граничными условиями (4). В результате получим:
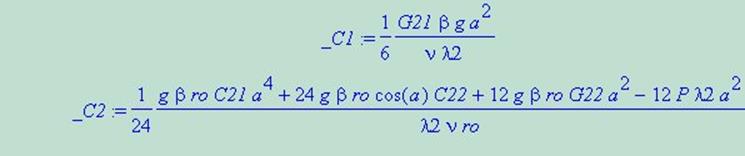
Рассмотрим несколько частных случаев:
Зададим a = 10, b=10, c=10, Tg1=300, Tg2 = 300, lambda1=0.9, lambda2=0.9, lambda3=0.9, alpha1=1, alpha2=1, P=10, g=9.81, G11=1, G12=1, G21=-1, G22=-1, G31=1, G32 = 1
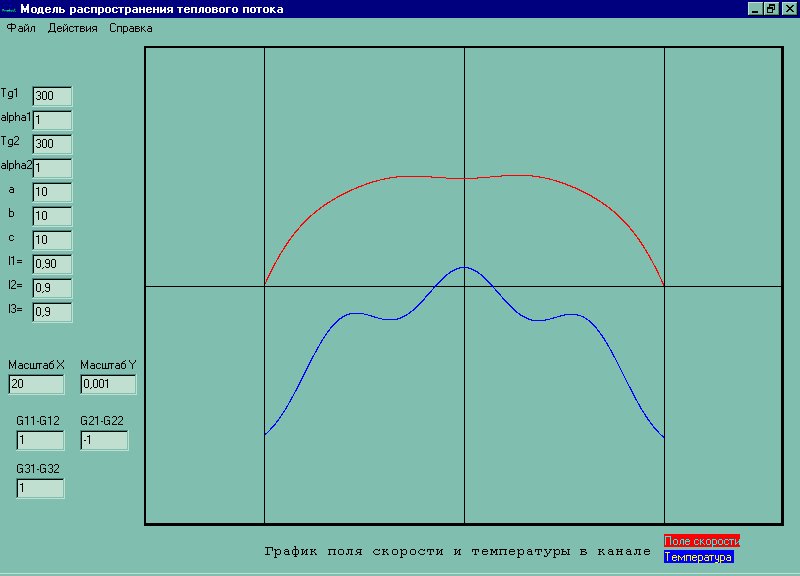
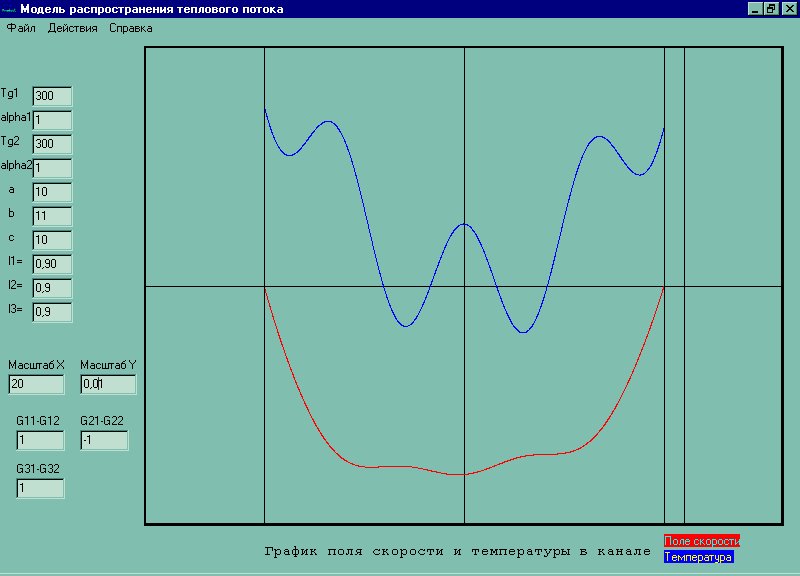
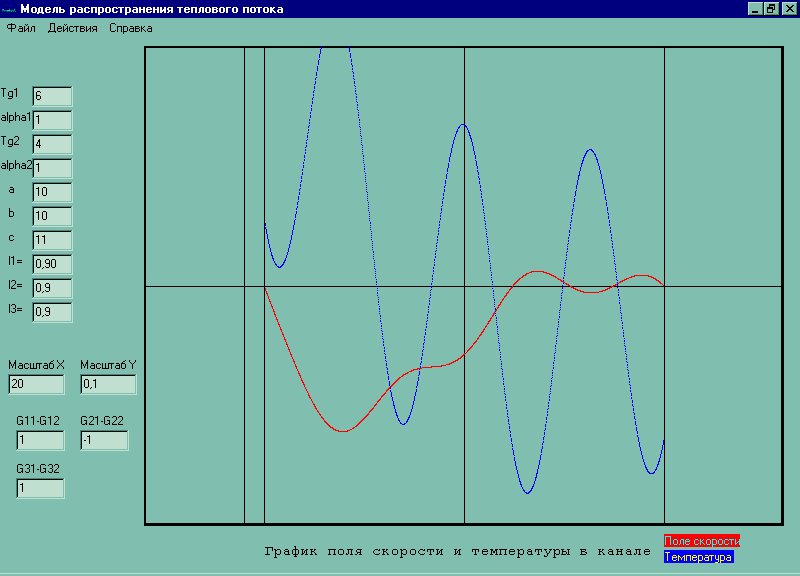
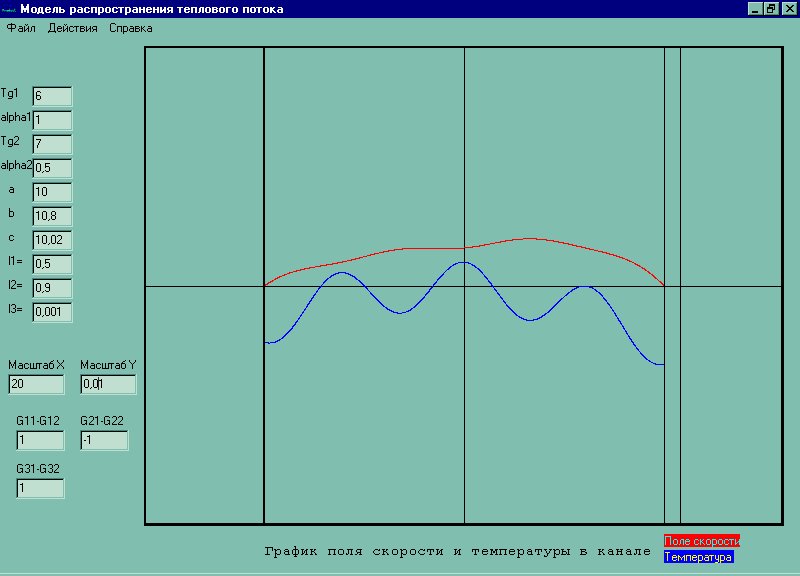
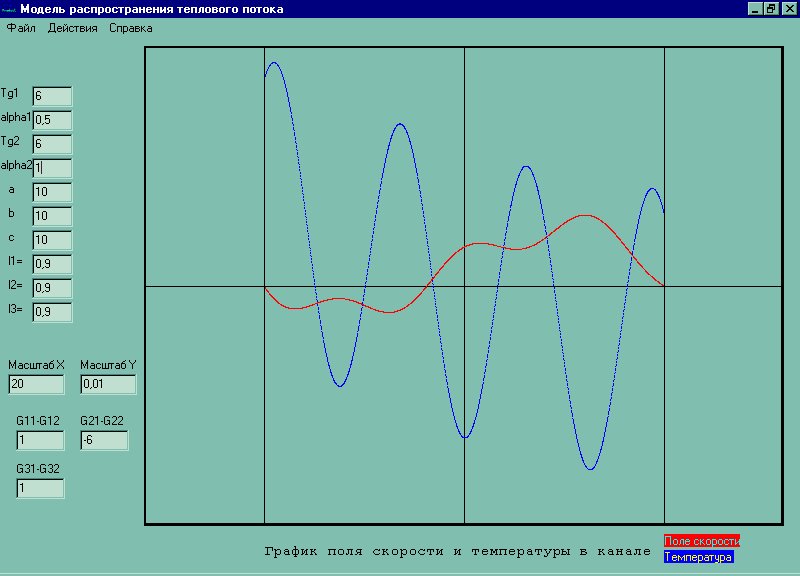
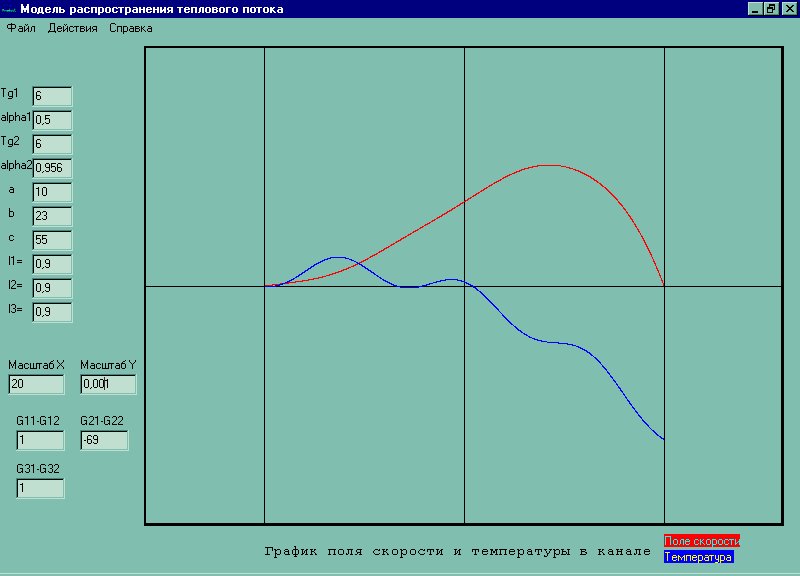
Тест на верность постановки модели: зададимся условиями когда мы знаем чего ожидать:
1) qvi=0
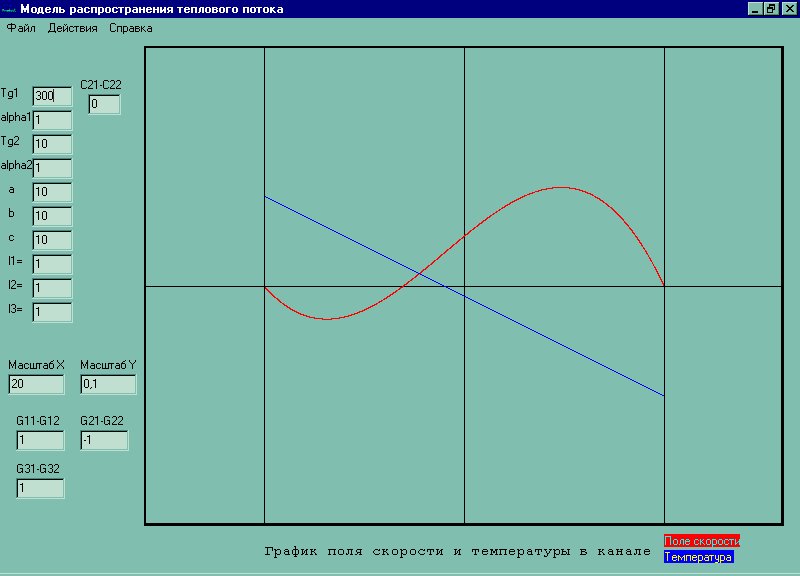
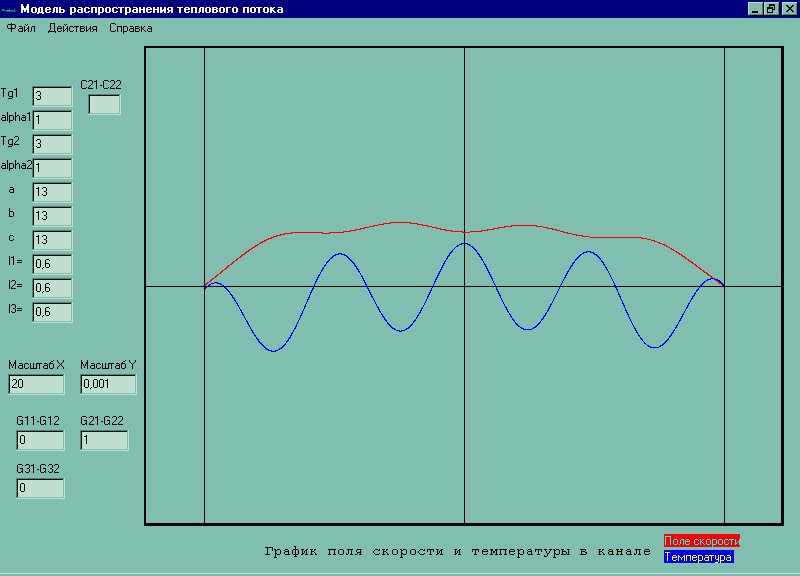
2) qv1=0, qv3=0;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.