Лабораторная работа №3.
Уравнение колебания струны.
Цель: написать программу, описывающую колебания струны.
![]() - длина струны
- длина струны
![]() -определяет форму струны в момент времени
-определяет форму струны в момент времени ![]() .
.
Предположим:
1.
все точки струны движутся перпендикулярно оси ![]() – поперечные колебания.
– поперечные колебания.
2. струна абсолютно гибкая, т.е. нет сопротивления изгибу.
3. силы напряжения направлены по касательной.
4. струна упруга, т.е. подчиняется закону Гука.
5.
струна упругая с линейной плотностью ![]() .
.
6.
на струну действуют внешние силы параллельные оси ![]() , и распределении сил задается функцией
, и распределении сил задается функцией ![]() .
.
Решение:
колебание струны описывается следующим уравнением.
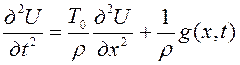 - одномерное волновое уравнение.
- одномерное волновое уравнение.
где,
![]() - сила напряжения действующая на нить.
- сила напряжения действующая на нить.
Начальные условия:
![]() – начальное положение нити.
– начальное положение нити.
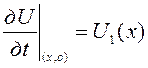 – начальная скорость в каждой точке.
– начальная скорость в каждой точке.
![]()
пусть
![]() без внешних
сил.
без внешних
сил.
Найти решение задачи численным методом.
Составим разностную сетку.
![]()
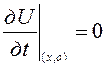
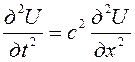 , где
, где 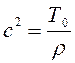
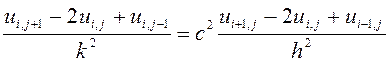
где
![]() -шаги координатной сетки по оси
-шаги координатной сетки по оси ![]() и по времени соответственно.
и по времени соответственно.
![]() , где
, где 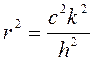
![]()
![]() ,
, ![]() , где
, где ![]() - количество разбиений по оси
- количество разбиений по оси ![]() и по времени соответственно.
и по времени соответственно.
из начального условия получим.
![]()
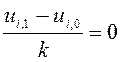 , следовательно
, следовательно ![]() , где
, где ![]()
Далее
прогонкой найдем все значения ![]()
Для
гарантирования устойчивой сходимости требуется чтобы ![]() .
.
Пример работы программы:
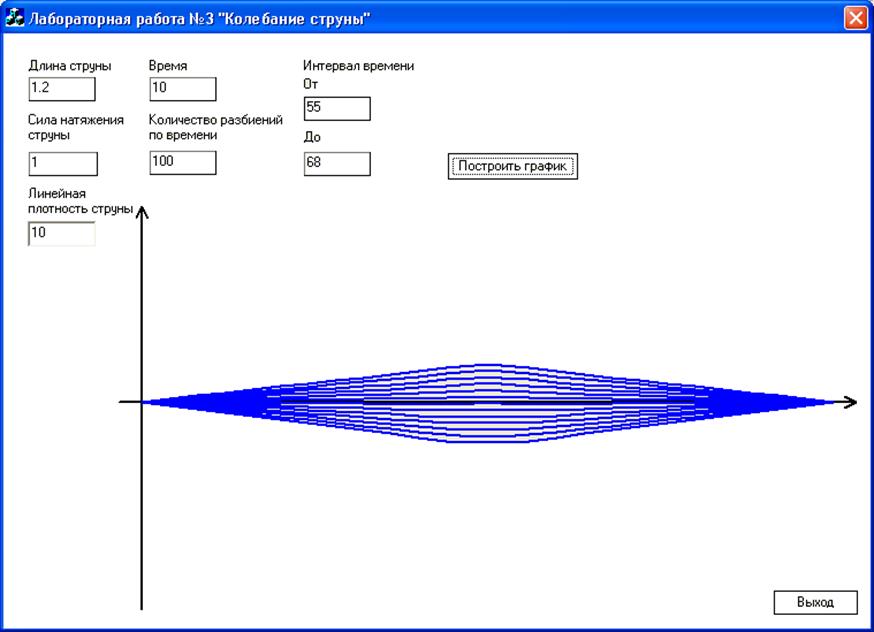
Описание программ:
- в ходе выполнения программы строится графика колебания струны по моментам времени:
- в программе можно задать интервал времени для отображения колебаний.
Вывод: В ходе работы была написана программа, описывающая уравнение колебания струны. Для нахождения алгоритма построения было найдено численное решение при помощи составления разностной сетки.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.