Решение системы дифференциальных уравнений описывающих численность двух видов хищников и жертвы, методом конечных разностей

Лабораторная работа №2

Модель Хищник-Жертва

Модель взаимодействия "хищник-жертва" независимо предложили в 1925-1927 гг. Лотка и Вольтерра. Два дифференциальных уравнения моделируют временную динамику численности двух биологических популяций жертвы N(t) и хищника M(t). Предполагается, что жертвы убывают при встречи с хищниками с коэффициентом С, а коэффициент прироста жертв при встречи с хищниками равен γ.

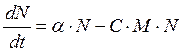
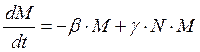
Начальные условия:

N(0) = N₀  - начальное количество жертв

M(0) = M₀ - начальное количество хищников

Для решения этой системы дифференциальных уравнений применим разностную  схему.

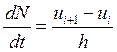, где h = T/n,  T – временной интервал , n – количество разбиений

Программа для нахождения численности хищника и жертв:

CClientDC dc(this);

CPen NewPen(PS_SOLID, 1, RGB(255,0,255));

dc.SelectObject(&NewPen);

dc.MoveTo(0,150);

dc.LineTo(600, 150);

dc.MoveTo(50,0);

dc.LineTo(50, 300);

int T = 100, n;

float alpha,  beta, r, C; 

float h = 0.01, N[90000], M[90000];

UpdateData(TRUE);

alpha = m_float1;

beta = m_float2;

r = m_float3;

C = m_float4;

n =T/h;

int Xcoord, Ycoord;

float Ncurrent=10, Nnext, Mnext;

float Mcurrent=15;

for (int i=0; i<n; i++){

Xcoord = i*h*10;

Ycoord = Ncurrent*4;

dc.SetPixel(50+Xcoord,150-Ycoord,RGB(255,0,0));

Ycoord = Mcurrent*4;

dc.SetPixel(50+Xcoord,150-Ycoord,RGB(255,255,0));

Nnext = (alpha*Ncurrent-C*Mcurrent*Ncurrent)*h+Ncurrent;

Mnext = (-beta*Mcurrent+r*Mcurrent*Ncurrent)*h+Mcurrent;

Ncurrent = Nnext;

Mcurrent = Mnext;

}

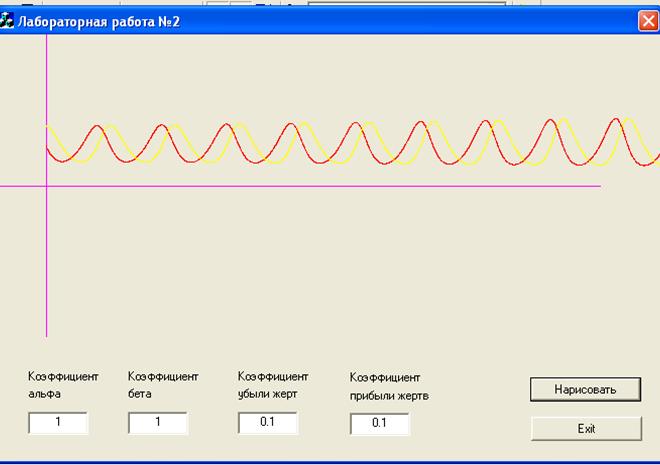Пример работы приложения:

Вывод: в лабораторной работе было решена система дифференциальных уравнений описывающих численность двух видов хищников и жертвы, методом конечных разностей.