Лабораторная работа №1
Математический маятник
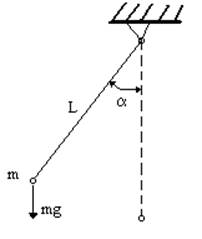
На нерастяжимой, невесомой нити длинной L подвешен груз массой m, груз откланяется на угол α. Записать дифференциальное уравнение средних колебаний маятника без учета действия внешних сил, сопротивления воздуха. Написать программу для решения дифференциального уравнения численным методом. Решить данное дифференциальное уравнение в программной среде MathCad. Сравнить результаты.
Решение
1. Составление дифференциального уравнения колебания маятника при средних колебаниях:
 с одной
стороны:
с одной
стороны:
момент инерции равен ![]()
угловое ускорение ![]()
а с другой стороны ![]()
получаем ![]() , где
, где ![]()
![]() , где
, где ![]()
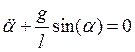
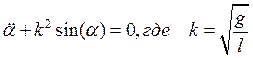
Решение дифференциального уравнения методом конечных разностей
Зададим начальные условия:
![]()
![]() где
h - шаг
где
h - шаг
Разностная схема имеет вид:
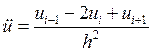
![]()
исходное уравнение перепишется в виде:
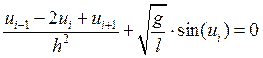
![]()
Решение будем искать на интервале (a,b) = T, откуда
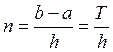
Составим программу:
{
int T = 100, n, alpha, v;
float h = 0.09, l = 10 ,u[90000], k ;
UpdateData(TRUE);
alpha = m_integer;
n =T/h;
k = l/9.8;
u[0] = alpha;
v = m_integer1;
u[1] = u[0]-v*h;
for (int i=1; i<=n-1;i++){
u[i+1] = 2*u[i] - h*h*k*sin(u[i]*3.14/180) - u[i-1];
}
CClientDC dc(this);
CPen NewPen(PS_SOLID, 1, RGB(255,0,255));
dc.SelectObject(&NewPen);
dc.MoveTo(0,150);
dc.LineTo(600, 150);
m_PrevX=0;
m_PrevY=u[0];
int y, b;
for (int j=1; j<=n;j++){
y = j*h*1.2;
b= u[j];
dc.MoveTo(50+m_PrevX, 150-m_PrevY);
dc.LineTo(50+y, 150-b);
m_PrevX=y;
m_PrevY=b;
}
}
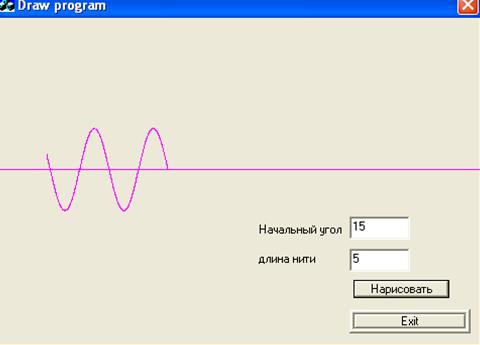 |
Решение в среде MathCad 2001
Для решения дифференциального уравнения в среде MathCad используется блок
Given/ Odesolve.
Пример решения дифференциального уравнения при начальных условиях: длина нити равна 5 а начальный угол 15.
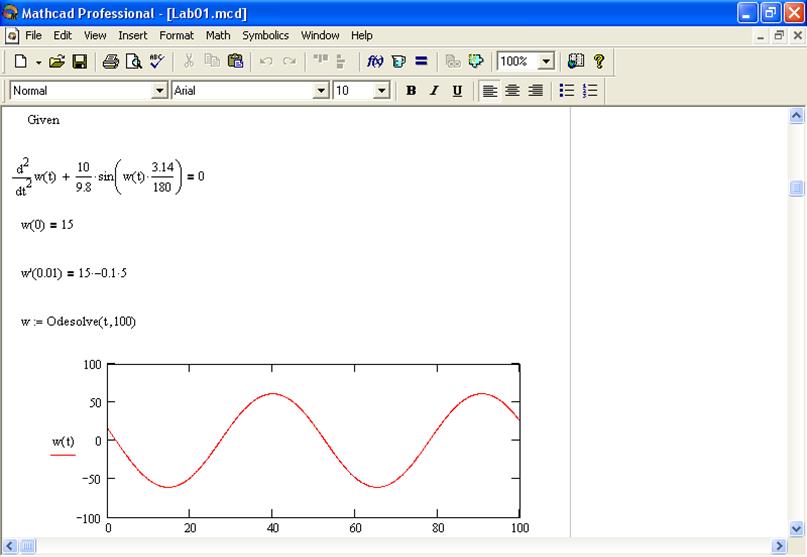
Вывод: в лабораторной работе было составлено уравнение колебания математического маятника, которое было решено численными способами: на основе программной среды MathCad 2001, и составления собственной программы для решения данного дифференциального уравнения. Как видно из графиков эти решения совпадают.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.