Построение эмпирических формул методом наименьших квадратов (МНК) средствами пакета Microsoft Excel, страница 9

            End;

          g:=0;

          For k:=1 to n do         {Матрица свободных членов}

            g:=g+a[k,i]*y[k];

          r[i,c+2]:=g;

          For j:=1 to c+2 do

           begin

              Write(d1, r[i,j]:13:5,'    ');

              Write( r[i,j]:13:5,'    ');

            end;

          WriteLn(d1);

          WriteLn;

        End;

      Gauss(c+1,r);

      WriteLn(d1,'Полученные коэффициенты:');

      WriteLn('Полученные коэффициенты:');

      For i:=1 to c+1 do

        begin

          WriteLn(d1,'    a',i,' = ', r[i,c+2]:10:5,'      ');

          WriteLn('    a',i,' = ', r[i,c+2]:10:5,'      ');

        end;

      WriteLn(d1);

      Writeln;

    End;

  Close(d1);

End.

Файл исходных данных “Danil.dat”

3.28 3.87 4.65 4.99 5.08 5.34 5.65 5.77 5.83 6.06 6.33 6.41 6.55 6.85 7.01 7.23 7.83 7.92 8.14 8.23 8.55 9.32 9.66 10.13 10.25

5.05 6.87 10.43 12.96 12.08 13.11 20.86 21.97 22.99 27.75 33.43 41.45 46.44 60.94 79.08 90.44 94.85 103.06 124.45 143.65 191.54 204.45 216.97 279.74 325.43

Вывод результатов.

Матрица A

     25.00000        170.93000       2189.99000   

    170.93000       1253.89050      18804.34470   

Полученные коэффициенты:

    a1 = -219.80073     

    a2 =   44.95997     

Матрица A

     25.00000        170.93000       1253.89050       2189.99000   

    170.93000       1253.89050       9762.47223      18804.34470   

   1253.89050       9762.47223      79858.01208     166256.74510   

Полученные коэффициенты:

    a1 =  143.68223     

    a2 =  -67.08789     

    a3 =    8.02723

Приложение.

Рисунки хода работы

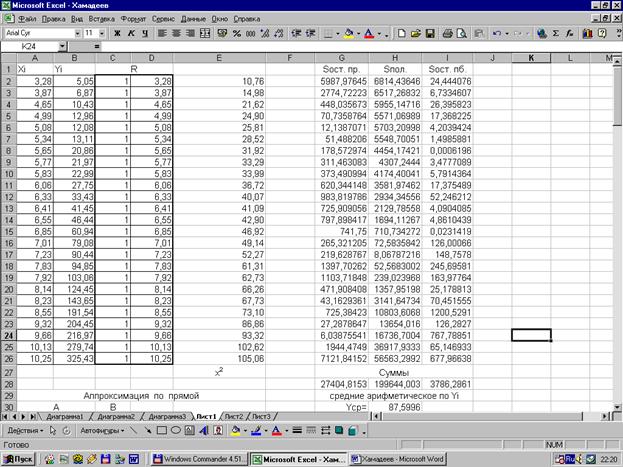
Рис. 6

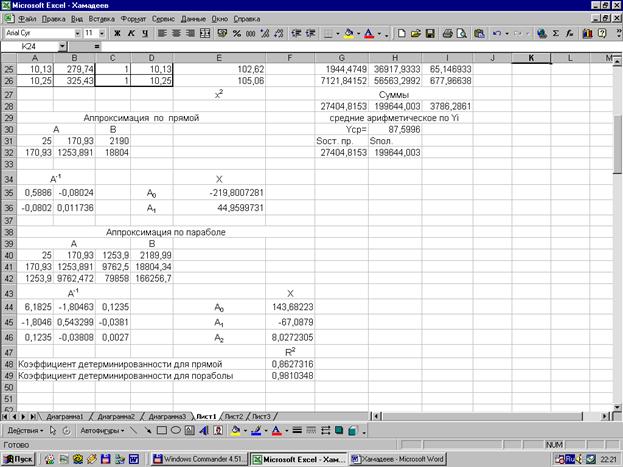
Рис. 7

Вывод.

Анализ результатов расчетов коэффициентов детерминированности для линейной, квадратичной  аппроксимаций показывает, что квадратичная аппроксимация наилучшим образом описывает экспериментальные данные.

Полученное при построении линии тренда значение коэффициента детерминированности для кубической функции 0,9812≈0,981 для квадратичной.

              Функция тренд даёт довольно точные значения. Программа на языке Паскаль дала такие же результаты при расчёте коэффициентов, что говорит о правильности проведенных расчетов, квадратичная лучше линейной, а кубическая лучше квадратичной. Окончательная зависимость для квадратичной выглядит следующим образом:

Библиографический список

1. Б.П. Демидович, И.А. Марон. Основы вычислительной математики. М.: Государственное издательство физико-математической литературы, 1963.

2. Информатика: Учебник / Под ред. проф. Н.В. Макаровой. М.: Финансы и статистика, 1997.

3. Информатика: Практикум по технологии работы на компьютере/ Под ред. проф. Н.В. Макаровой. М.: Финансы и статистика, 1997.

4. В.Б. Комягин. Программирование в Excel5 и Excel7 на языке Visual Basic. М.: Радио и связь, 1996.

5. Н. Николь, Р.Альбрехт. Excel 5.0. Электронные таблицы. М.: Изд. “ЭКОМ”, 1996.