Построение эмпирических формул методом наименьших квадратов (МНК) средствами пакета Microsoft Excel, страница 7

Поясним как составили таблицу 8:

Шаг 1 В ячейку В48 вводим формулу =1-G28/H28.

Шаг 2 В ячейку В49 вводим формулу =1-I28/H28.

Вывод

Анализ результатов расчетов показывает, что наилучшим образом описывает экспериментальные данные парабола так как её коэффициент  R²=0,9810348 наиболее близок к единице, поэтому следует выбрать уравнение :

II Решение задачи графическим методом используя функцию  EXCEL –“ТРЕНД”.

Введение.

Рассмотрим результаты эксперимента, приведенные в исследованном выше примере.

Исследуем характер зависимости в два  этапа:

·  Построим график зависимости.

·  Построим линию тренда.

Решение

Построение графика зависимости.

1.  Выделим интервал А2:В26.

2.  Вызовем Мастера диаграмм, нажав соответствующую кнопку на панели инструментов.

3.  Используя мышь, выделим область для встроенной диаграммы.

4.  На 1 шаге в диалоговом окне Мастера диаграмм интервал А2:В26 должен быть указан. Нажимаем Шаг>.

5.  На 2 шаге выберем  тип диаграммы XY-точечная. Нажмем Шаг>.

6.  На 3 шаге выберем 1 тип автоформата. Нажмем Шаг>

7.  На 4 шаге укажем следующие параметры:

8.  Отводим 1 столбец для данных по оси Х;  отведем 1 строку для текста легенды. Нажмем Шаг>.

9.  На 5 шаге в окне “Название диаграммы: «введем заголовок  “Линейная аппроксимация”; в окне “Категорий [X]:” введем “x”; в окне “Значений [Y]:” введем y. Нажмем Закончить.

Построение линии тренда

Для построения линии тренда  выполняем следующую последовательность действий:

1.  Дважды щелкнем по диаграмме. Диаграмма активизируется.

2.  Щелкнем по графику непосредственно в одну из изображенных точек. Сам график активизируется, его окраска изменится.

3.  Вставляем линию тренда, воспользуемся менюDВставкаDЛиния тренда.

4.  Появится диалоговое окно “Линия тренда” выберем на вкладке “Тип”   линейный тип и перейдем к вкладке “Параметры”.

На вкладке “Параметры”  потребуем показывать уравнение тренда на диаграмме и показывать значение R²,  поставив их  в соответствующие клетки. Нажимаем кнопку ОК.

Графики и уравнения кривых, коэффициенты детерминированности

На диаграмме появится линия тренда  с соответствующим уравнением. Также изменится легенда. При желании текстовое поле с уравнением и значением  R², а также название координат x и y. Можно  очень быстро получать решение задачи данным методом, но очень ограниченным типом функций.

Произведём построение графиков для функций до параболы третьей степени.

Вывод

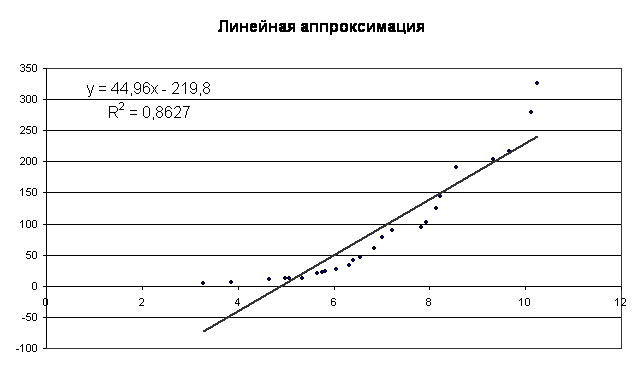
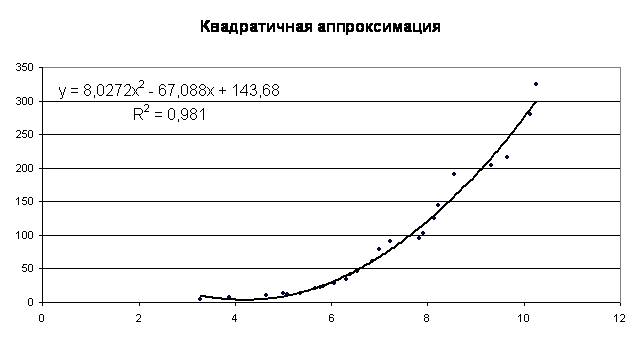
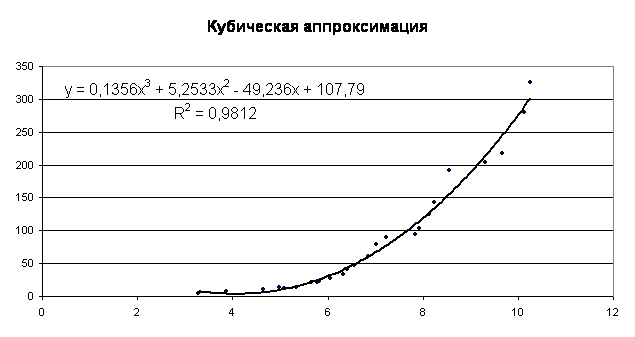
Сравнивая  результаты , полученные при  вычислении в Microsoft Excel  видим, что они полностью совпадают с вычислениями, проведенными с помощью функции EXCEL – “ТРЕНД”. Это указывает на то, что вычисления верны.

В ходе решения поучили, что наилучшие уравнение аппроксимации кубической парабола  коэффициент детерминированности наиболее близок к единице   и составляет. аппроксимация по параболе будет хуже так как коэффициент детерминированности ниже, чем у кубической параболы.

III  Программа на языке программирования Pascal для решения задачи.