Построение эмпирических формул методом наименьших квадратов (МНК) средствами пакета Microsoft Excel, страница 5

Полученная функция у лучше всего аппроксимирует заданную зависимость, что видно на рис. 2

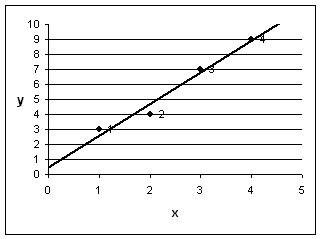
рис. 2

Аналогично получаем систему для квадратичной аппроксимации:

                                           (8)

Аналогичным методом можно получить кривые высших  порядков, но степень точности не очень высокая начиная с седьмой степени. Поэтому дальше используются другие методы.

Решение задачи.

Для проведения расчетов в матричной форме, исходные данные целесообразно расположить в виде таблицы 3, используя  средства табличного процессора Microsoft Excel.

                                                                                              Таблица 3.

Таблица 2 составлена в 8 шагов:

Шаг 1. В ячейки A2:A26 заносим значения .

Шаг 2. В ячейки B2:B26 заносим значения .

Шаг 3. В ячейку C2 вводим 1.

Шаг 4. В ячейки C3:C26 это значение копируется.

Шаг 5. В ячейку D2 вводим формулу =A2.

Шаг 6. В ячейки D3:D26 эта формула копируется.

Шаг 7. В ячейку E2 вводим формулу =A2^2.

Шаг 8. В ячейки E3:E26 эта формула копируется.

Линейная аппроксимация.

Аппроксимируем функцию линейной функцией . Для определения коэффициентов  и  воспользуемся системой (4). Используя иcходные данные таблицы 3, расположенные в ячейках A2:F26, запишем систему, воспользовавшись формулами (4) в виде:

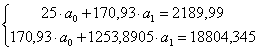                            (11)

решив которую, получим  и .

Таким образом, линейная аппроксимация имеет вид

 .                                     (12)

Решение системы (11) проводили, пользуясь средствами Microsoft Excel. Результаты представлены в таблице 4.

                                                  Таблица 4

Таблица 4 сформирована в 4 шага:

Шаг 1 В ячейках A31:B32 записана формула {=МУМНОЖ(ТРАНСП(C2:D26);C2:D26)}.

Шаг 2 В ячейках C31:C32 записана формула {=МУМНОЖ(ТРАНСП(C2:D26);B2:B26)}.

Шаг 3 В ячейках A35:B36 записана формула {=МОБР(А31:В32)}.

Шаг 4 В ячейках E35:E36 записана формула {=МУМНОЖ(A35:B36;C31:C32)}.

Квадратичная аппроксимация.

Аппроксимируем функцию  квадратичной функцией . Для определения коэффициентов ,  и  воспользуемся системой (5). Используя исходные данные таблицы 2, расположенные  в ячейках A1:Е26 запишем систему, воспользовавшись формулами (5) в виде (cм таблицу 3):

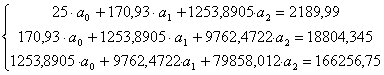                             (13)

решив которую, получим , и .