Построение эмпирических формул методом наименьших квадратов (МНК) средствами пакета Microsoft Excel, страница 4

I Решение задачи с использованием пакета MS Exсel.

Метод наименьших квадратов (МНК) разберём на примере.

Пример:

Пусть задана функция в виде таблицы:

Таблица 2

x	1	2	3	4
y	3	4	7	9

Решение:

Построим график этой функции (рис. 1):

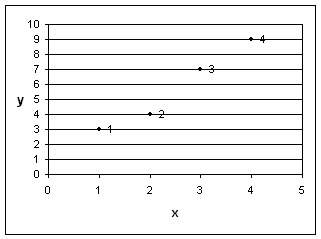
Рис. 1

Аппроксимируем эту таблично заданную функцию непрерывной, так чтобы сумма квадратов невязок была бы минимальной, т. е:

(1)

В качестве аппроксимируемой функции выберем прямую:

(2)

Потребуем, чтобы искомая прямая проходила через точки 1, 2, 3, 4. В итоге получим систему уравнений:

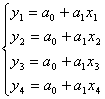(3)

Эта система переопределена. Переопределённые системы решаются стандартным методом:

1. Записываем систему уравнений (3) в матричной форме:

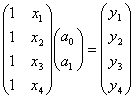(4)

или RХ=Y (4а)

где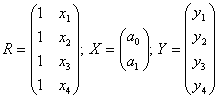

2. Систему уравнений (4а) слеваумножаем на :

(5)

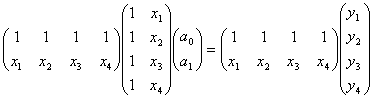или (5а)

после простых преобразований получим:

(6)

или (6а)

где

Матрица симметричная. Можно показать, что она положительно определена, но плохо обусловлена. В рассмотренном случае окончательно получаем:

(7)

где n количество пар значений (в нашем случае 4). Подставив в систему уравнений (7) исходные данные, получаем:

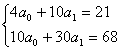
Эту систему решим методом Крамера:

Подставив полученные в уравнение (2), окончательно получим:

1 2 3 4 5 6 7 8 9