Четырехмерный мир (пространство Минковского).
Интервал. Расстояния и временные промежутки в классической механике являются инвариантными величинами – одинаковыми во всех ИСО. В теории относительности они уже не обладают этим свойством, зато в ней появляется ряд новых инвариантных величин, прежде всего скорость света c. К инвариантам относятся также собственное время, масса покоя, электрический заряд и др. Весьма важной инвариантной величиной является интервал Ds между двумя событиями, квадрат которого определяется как
![]() ,
где Dt – промежуток времени
между событиями, Dr – расстояние
между точками, в которых происходят данные события (
,
где Dt – промежуток времени
между событиями, Dr – расстояние
между точками, в которых происходят данные события (![]() ).
).
В инвариантности интервала можно легко убедиться, вычислив его непосредственно в K¢- и K-системах отсчета. Воспользовавшись преобразованиями Лоренца (Л16-6) запишем
![]() .
.
Учитывая, что ![]() и
и ![]() , заключаем, что интервал является
инвариантной величиной. Инвариантность интервала играет фундаментальную роль в
теории относительности и служит весьма эффективным инструментом при анализе и
решении многих вопросов.
, заключаем, что интервал является
инвариантной величиной. Инвариантность интервала играет фундаментальную роль в
теории относительности и служит весьма эффективным инструментом при анализе и
решении многих вопросов.
Типы интервалов. В зависимости от того, какая
составляющая в интервале преобладает, пространственная или временная,
соответствующие интервалы называют: пространственноподобными (![]() ), времениподобными (
), времениподобными (![]() ). Кроме этих двух типов интервалов
существует еще третий – светоподобный (
). Кроме этих двух типов интервалов
существует еще третий – светоподобный (![]() ).
).
Если интервал между двумя событиями пространственноподобный,
то всегда можно найти такую K¢-систему
отсчета, в которой оба события происходят одновременно (![]() ).
).
Если же интервал времениподобный, то всегда можно найти
такую K¢-систему отсчета, в
которой оба события происходят в одной точке (![]() ).
).
В случае пространственноподобных интервалов ![]() , т.е. ни в одной системе отсчета события
не могут оказать влияния друг на друга, даже если бы связь между событиями
осуществлялась с предельной скоростью c. Иначе
обстоит дело в случае времениподобных или светоподобных интервалов, для которых
, т.е. ни в одной системе отсчета события
не могут оказать влияния друг на друга, даже если бы связь между событиями
осуществлялась с предельной скоростью c. Иначе
обстоит дело в случае времениподобных или светоподобных интервалов, для которых
![]() . Следовательно, события, разделенные
времениподобными или светоподобными интервалами, могут быть причинно-связанными
друг с другом.
. Следовательно, события, разделенные
времениподобными или светоподобными интервалами, могут быть причинно-связанными
друг с другом.
Пространство Минковского. В связи с инвариантностью
интервала целесообразно не разделять пространство и время, а рассматривать их
вместе как четырехмерное пространство-время. Совокупность четырех величин
![]() будем рассматривать как четырехвектор
события (мировой точки) R в пространстве, называемом
пространством Минковского, а величину
будем рассматривать как четырехвектор
события (мировой точки) R в пространстве, называемом
пространством Минковского, а величину
![]() как квадрат его длины. Квадрат длины R, как следует из
сопоставления его с интервалом, является четырехскаляром (инвариантом).
Четырехскаляром (инвариантом) в общем случае называется величина, не зависящая
от выбора ИСО
как квадрат его длины. Квадрат длины R, как следует из
сопоставления его с интервалом, является четырехскаляром (инвариантом).
Четырехскаляром (инвариантом) в общем случае называется величина, не зависящая
от выбора ИСО ![]() . В свою очередь четырехвектором
называется совокупность четырех величин
. В свою очередь четырехвектором
называется совокупность четырех величин ![]() ,
которая при переходе из одной ИСО в другую преобразуется так же, как и
компоненты четырехвектора события, т.е. для компонент четырехвектора A справедливы прямые (и
обратные) преобразования Лоренца
,
которая при переходе из одной ИСО в другую преобразуется так же, как и
компоненты четырехвектора события, т.е. для компонент четырехвектора A справедливы прямые (и
обратные) преобразования Лоренца
![]() ,
, ![]() ,
, ![]() ,
, ![]() , (1а)
, (1а)
![]() ,
, ![]() ,
, ![]() ,
, ![]() , (1б)
где
, (1б)
где ![]() ,
, ![]() .
.
Нетрудно установить, что квадрат длины четырехвектора ![]() является четырехскаляром. Как и интервалы
4-векторы делятся на пространственноподобные (
является четырехскаляром. Как и интервалы
4-векторы делятся на пространственноподобные (![]() ) и
времениподобные (
) и
времениподобные (![]() ).
).
Удобство четырехвекторов состоит в том, что их можно
складывать и умножать на числа по правилам, аналогичным правилам действий над
векторами в трехмерном пространстве. Точно так же запись ![]() означает равенство соответствующих
компонент четырехвекторов, причем равенство
означает равенство соответствующих
компонент четырехвекторов, причем равенство ![]() сохраняется
в любой другой ИСО, хотя каждая из компонент при переходе в эту ИСО может
измениться.
сохраняется
в любой другой ИСО, хотя каждая из компонент при переходе в эту ИСО может
измениться.
Аппарат четырехвекторов позволяет наиболее просто и единообразно находить законы преобразования кинематических и динамических величин. Особую роль четырехвектора и четырехскаляры приобретают при формулировке фундаментальных законов природы. Согласно принципу относительности объективные законы физики должны сохранять свою форму во всех ИСО. Это условие автоматически выполняется, если они записываются в четырехвекторной или четырехскалярной форме.
Построение четырехвекторов начнем с 4-скорости и 4-ускорения. Движение материальной точки в пространстве Минковского можно описать в виде функциональной зависимости четырех ее координат (времени и трех пространственных координат) от собственного времени тела
![]() .
Естественно тогда определить компоненты 4-скорости как
.
Естественно тогда определить компоненты 4-скорости как
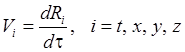 .
Действительно, указанные величины преобразуются как компоненты 4-вектора,
поскольку числитель является дифференциалом четырехвектора, а знаменатель –
дифференциалом четырехскаляра. Связь дифференциалов собственного времени и
времени в ИСО, относительно которой рассматривается движение, имеет вид
.
Действительно, указанные величины преобразуются как компоненты 4-вектора,
поскольку числитель является дифференциалом четырехвектора, а знаменатель –
дифференциалом четырехскаляра. Связь дифференциалов собственного времени и
времени в ИСО, относительно которой рассматривается движение, имеет вид
![]() ,
где
,
где ![]() , а
, а ![]() (v
– скорость тела). Используя эту связь, раскрываем смысл компонент 4-скорости
(v
– скорость тела). Используя эту связь, раскрываем смысл компонент 4-скорости
![]() ,
где
,
где ![]() – компоненты обычной трехмерной скорости v,
или в компактном виде
– компоненты обычной трехмерной скорости v,
или в компактном виде
![]() .
Квадрат длины 4-скорости является инвариантом равным
.
Квадрат длины 4-скорости является инвариантом равным ![]()
![]() .
.
4-скорость преобразуется при переходе из одной ИСО к другой согласно формулам (1а). Запишем 4-скорость в K- и K¢-системах соответственно как
![]() ,
, ![]() .
На основании преобразований Лоренца (1а)
.
На основании преобразований Лоренца (1а)
![]() ,
, ![]() ,
, ![]() ,
, ![]() . (2)
Из последнего равенства (2) следует, что
. (2)
Из последнего равенства (2) следует, что
![]() .
После несложных преобразований остальных выражений (2) получим
.
После несложных преобразований остальных выражений (2) получим
 ,
,  ,
, 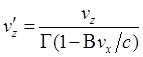 . (3)
Эти формулы выражают релятивистский закон преобразования скоростей. При
малых скоростях (
. (3)
Эти формулы выражают релятивистский закон преобразования скоростей. При
малых скоростях (![]() и
и ![]() ) они
переходят, как нетрудно убедиться, в формулы преобразования скоростей
классической механики
) они
переходят, как нетрудно убедиться, в формулы преобразования скоростей
классической механики
![]() ,
,
![]() ,
, ![]() ,
или в векторном виде
,
или в векторном виде
![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.