Четырехмерный мир (пространство Минковского). Релятивистская динамика, страница 2

Проверим непосредственно, что релятивистские формулы преобразования скоростей соответствуют второму постулату Эйнштейна о неизменности скорости света c во всех ИСО. Ограничимся случаем движения луча света в K-системе вдоль оси X. В K¢-системе луч будет двигаться в том же направлении, вдоль оси X¢. Поскольку  и , то из (3) следует

 .

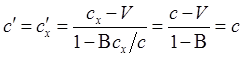Постоянство скорости света легко устанавливается и в общем случае. При этом направления лучей в двух инерциальных системах будет, вообще говоря, различно.

Четырехмерное ускорение определим в соответствии с обычным трехмерным подходом

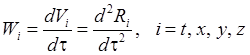 . Компоненты 4-ускорения можно выразить через компоненты трехмерных векторов v и . Для пространственных компонент получаем

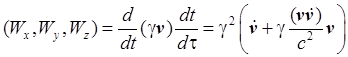 . При выводе формулы использовались  и . Временная компонента ускорения

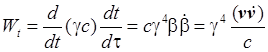 . В сопутствующей ИСО, в которой частица покоится ()

 ,  ,                                                  (4) т.е. пространственные слагающие 4-ускорения совпадают с обычными трехмерными компонентами ускорения, а временная составляющая обращается в ноль. Из (4) видно, что , поэтому 4-ускорение пространственноподобный четырехвектор.

Релятивистская динамика

При наблюдении за движением тел обращает внимание то, что чем больше масса и скорость движущегося тела, тем более сильный эффект возникает при его соударении с другими телами. Так, например, при движении ядра его разрушительная сила тем больше, чем больше его масса и скорость; метеорит, достигший поверхности Земли, проникает в грунт тем больше, чем больше масса и скорость метеорита.

Далее, при наблюдении за движением шаров до столкновения и после него, можно заметить, что если в результате столкновения движение одного из шаров «уменьшилось», то движение второго шара «увеличилось» и притом тем более, чем значительнее «уменьшилось» движение первого шара. Представляется поэтому, что хотя мера движения каждого из шаров меняется при соударении, сумма таких мер для обоих шаров остается неизменной, т.е. происходит «обмен движением» при сохранении меры движения для системы в целом.

Подобные закономерности нашли выражение в понятиях количества движения (импульса) и кинетической энергии как формы энергии, связанной с движением. Соответствующие законы сохранения – законы сохранения импульса и энергии –занимают центральное место в классической механике и физике вообще.

Развитие физики подтверждает, что законы сохранения позволяют в концентрированном виде выражать наиболее общие свойства материальных тел (объектов) и их взаимодействий. Учитывая центральную роль, которую играет закон сохранения импульса в классической механике, в теории относительности в качестве ключевого момента принимается идея его сохранения, и потом уже находится выражение для самого импульса.

Релятивистский импульс. Как следует определить импульс частицы? Оказывается импульс можно установить, не обращаясь к эксперименту, с помощью общих соображений о его свойствах и требования сохранения полного импульса во всех ИСО

 .                                                           (5)

В классической механике импульс определялся как , где m – масса частицы, а v – ее скорость. Определенный таким образом импульс хорош тем, что импульс системы сохраняется при соударениях частиц малой энергии. Однако он не сохраняется, когда сталкивающиеся частицы обладают большими скоростями (в этом можно убедится на примере упругого столкновения).

Как видно, классический импульс – векторная величина, которая определяется только состоянием движения самой частицы. Будем предполагать, что это свойство сохраняется и при больших скоростях движения.