Четырехмерный мир (пространство Минковского). Релятивистская динамика, страница 4

Релятивистская энергия. Обсудим смысл временной компоненты 4-импульса. Введем в рассмотрение величину E равную произведению временной компоненты 4-импульса частицы на скорость света

 .                                                              (8) Эту величину можно назвать энергией. Во-первых, потому что она имеет размерность энергии. Во-вторых, что наиболее существенно, потому что сумма данных величин сохраняется при всех столкновениях. Доказательство того, сумма значений E всех частиц подчиняется закону сохранения, базируется на простом соображении: если три пространственные компоненты полного 4-импульса сохраняются во всех системах отсчета, то его временная компонента (а значит и суммарная E) тоже сохраняется. В противном случае сохранение импульса было бы невозможным.

Таким образом, сохранение полного импульса частиц приводит к сопутствующему закону, – закону сохранения энергии справедливому во всех ИСО

 ,                                                           (9) где  определяется выражением (8) и называется полной релятивистской энергией частицы.

При малых скоростях выражение для релятивистской энергии можно разложить в ряд по степеням v, пользуясь формулой Тейлора,

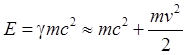 . Таким образом, в пределе малых скоростей релятивистская энергия складывается из классического выражения кинетической энергии и добавочного слагаемого . Этот добавочный член называют энергией покоя

 .                                                            (10) С момента получения Эйнштейном в 1905 г. эта формула нашла огромное число подтверждений, и одно из них – существование атомной бомбы.

В теории относительности определение кинетической энергии является тем же самым, что и в классической механике: кинетическая энергия – это энергия, обусловленная движением частицы. Для свободной частицы ее можно получить, вычитая из полной энергии энергию покоя

 .                                                 (11) При малых скоростях (11) сводится к классическому выражению .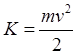

В связи с тем, что временная компонента 4-импульса имеет непосредственное отношение к энергии частицы, естественно назвать P 4-вектором энергии-импульса и записать его как

 . Из того, что квадрат 4-скорости , непосредственно вытекает

 .                                                (12) Таким образом, вектор энергии-импульса свободной частицы является времениподобным вектором.

Релятивистская сила. В теории относительности сила носит вспомогательную функцию. Это связано с тем, что взаимодействия распространяются с конечной скоростью, не превышающей скорость света. Поэтому невозможно определить силу так, чтобы для двух взаимодействующих частиц выполнялся третий закон Ньютона (важное свойство силы). Только в случаях локального взаимодействия, таких как взаимодействие частицы с полем или движение тела переменной массы (ракеты), можно записать  и , где  – импульс частицы (ракеты),  – импульс поля (отработанных газов).

На этом основании целесообразно определить силу выражением

 . Следует отметить, что при таком определении величина и направление силы будут зависеть от скорости движущегося наблюдателя, тогда как в классической механике сила не зависела от скорости наблюдателя. Эта зависимость приводит к интересным эффектам, например, к возникновению магнитной силы в электромагнитных взаимодействиях.

Для построения 4-вектора силы, которую иногда называют силой Минковского, рассмотрим 4-вектор , где t – собственное время частицы. С помощью () легко перейти собственного времени к обычному