Оптика: Методические указания по лабораторному практикуму, страница 17

Направления электрических векторов обыкновенного и необыкновенного лучей взаимно–перпендикулярны. И эти лучи распространяются в одном направлении, но с разными скоростями. В связи с этим по прохождении через пластинку между ними возникает разность хода:

ΔL = (n_o - n_e)d,                                                           (7)

где d – толщина кристаллической пластинки, n_o и n_e показатели преломления обыкновенного и необыкновенного лучей (индексом «о» будем в дальнейшем обозначать обыкновенную волну; индексом «е» - необыкновенную).

Как уже отмечалось ранее при наличии разности хода волны могут интерферировать только в том случае, если они когерентны. Если падающее на кристалл излучение не поляризовано,  о- и е- волны испускаются разными группами атомов (не согласованно), поэтому когерентности нет. Если же на кристалл падает линейно поляризованный свет, то волна разделяется между о- и е- волнами в пропорции, которая зависит от ориентации плоскости колебаний. Поэтому возникающие о- и е- компоненты когерентны и способны интерферировать.

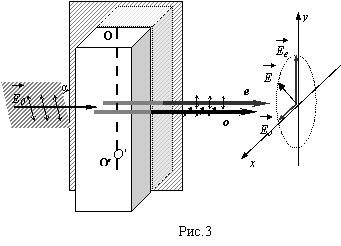
Из теории сложения колебаний известно, что, при сложении взаимно перпендикулярных колебаний одинаковой частоты, конец результирующего вектора  движется по эллипсу (рис.3):

x²/ E_о² – (2 xy/ E_оE_е) cos (δφ) + y²/ E_е² = sin² (δφ),

где δφ - сдвиг фаз колебаний на выходе из пластинки кристалла,
x и y - координаты конца результирующего вектора : x º E_x,  
y º E_y. Нас интересует случай, когда эллипс ориентирован своими полуосями по осям Оx  и  Оy (Оу лежит в главной плоскости кристалла), при этом E_o  и E_e  являются полуосями эллипса. Это наблюдается, если выполнено условие для разности фаз: ,   k =0, 1, 2, … Уравнение эллипса преобразуется при этом к виду:

E_x²/ E_о² + E_y²/ E_e² = 1.

Разность фаз колебаний связана с разностью хода лучей:
δφ = .. Используя  (7), получаем:

d (n_o - n_e) = ± (λ₀ / 4 + k λ).                                                           (8)

Здесь "+" соответствует отрицательным кристаллам (n_o > n_e),
"-" – положительным кристаллам (n_o < n_e). Таким образом, если толщина пластины, вырезанной вдоль оптической оси, удовлетворяет (8), результатом будет эллиптическая поляризация выходящего излучения. Такая пластина носит название четвертьволновой или  пластины λ/4.

Как добиться циркулярной(круговой) поляризации излучения? Эллипс превращается в окружность при условии равенства полуосей эллипса, т.е. E_o = E_e º E. Этого достигают, ориентируя четвертьволновую пластину оптической осью под углом α = 45° к плоскости колебаний падающего излучения. При этом компоненты результирующего вектора  удовлетворяют уравнению окружности: E_x² + E_y² = E².