Структурный анализ и метрический синтез рычажных механизмов

выявить число, класс, вид и порядок структурных групп звеньев, а также число и подвижность первичных (элементарных) механизмов;

10) записать формулу состава структуры механизма;

11) произвести проверку полученных  результатов;

12)определить класс механизма;

Задание 3. для плоского рычажного механизма.

1)  выбрать масштабный коэффициент длины;

2) перевести все заданные геометрические параметры механизма, имеющие размерность длин (м) в масштабный коэффициент;

3) построить кинематическую схему механизма для заданного положения кривошипа.

Задание 1.

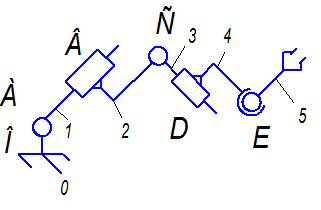
Рисунок 1 – Схема механизма промышленного манипулятора

Структурная схема рассматриваемого механизма содержит пять подвижных звеньев n=5.

Таблица 1

№	Номера звеньев/ название	Схема	Класс/ подвижность	Вид контакта/ замыкание
1	0 – 1/ вращательная		5/1	Поверхность (низшая)/ геометрическое
2	1 – 2/ поступательная		5/1	Поверхность (низшая)/ геометрическое
3	2 – 3/ вращательная		5/1	Поверхность (низшая)/ геометрическое
4	3 – 4/ поступательная		5/1	Поверхность (низшая)/ геометрическое
5	4 – 5/ сферическая		3/3	Поверхность (низшая)/ геометрическое

Кинематическая цепь одна, простая, не замкнутая.

Количество элементов стойки равно единице.

Подвижность пространственного механизма определяется с помощью структурной формулы Сомова-Малышева:

W=6n-5p₅-4p₄-3p₃-2p₂-p₁,                                     (1)

где     n – число подвижных звеньев механизма;

p_5, p_4, p_3, p_2, p₁ – число кинематических пар соответственно пятого, четвертого, третьего, второго, первого классов.

Из таблицы №1 следует, что n=5, p₅=4_, p₄=0_, p₃=1_, p₂=0_, p₁=0. Подставляем численные данные в формулу (1)

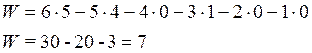
Считая схват – 5 (выходное звено) неподвижным имеем

,

Число кинематических пар остается прежнее p₅=4_, p₄=0_, p₃=1_, p₂=0_, p₁=0, тогда маневренность механизма будет определяться по следующей формуле

                                   (2)

Проверка осуществляется по следующей формуле:

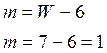
Задание 2. структурная схема плоского рычажного механизма представлена на рис. 2.

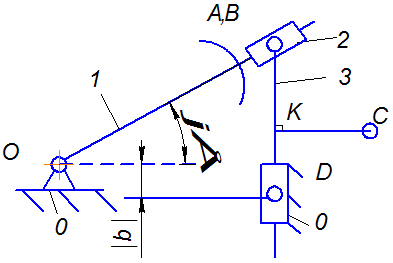
Рисунок 2 – схема плоского рычажного механизма

Структурная схема рассматриваемого механизма содержит три  подвижных звена n=3.

Таблица 2

№	Номера звеньев/ название	Схема	Класс/ подвижность	Вид контакта/ замыкание
1	0 – 1/ вращательная		5/1	Поверхность (низшая)/ геометрическое
2	1 – 2/ поступательная		5/1	Поверхность (низшая)/ геометрическое
3	2 – 3/ вращательная		5/1	Поверхность (низшая)/ геометрическое
4	3 – 0/ поступательная		5/1	Поверхность (низшая)/ геометрическое

Кинематическая цепь одна, простая, замкнутая.

Количество элементов стойки равно двум.

В структуре механизма дефектов нет.

Подвижность плоского механизма определяется с помощью структурной формулы Чебышева:

                                           (3)

где     n – число подвижных звеньев механизма;

         p_5, p_4, – число кинематических пар соответственно пятого, четвертого, классов.

Из таблицы №2 следует, что n=3, p₅=4_, p₄=0. Подставляем выявленные значения коэффициентов в формулу (3)

,

Для выявления числа структурных групп и подвижности первичных механизмов используем структурную классификацию механизмов профессора Ассура.

Первая группа звеньев 2 – 3 рис. 3.

 

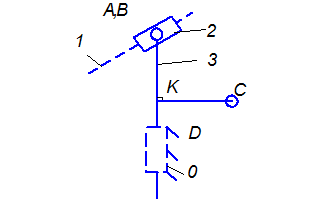
Рисунок 3 – первой структурной группы Ассура

Данная группа состоит из двух подвижных звеньев:

          камень 2 и кулиса 3;

двух поводков:

          кулиса 1 и стойка 0;

и трех кинематических пар:

          1 – 2 поступательная пара пятого класса;

          2 – 3 вращательная пара пятого класса;

          3 – 0 поступательная пара пятого класса;

Тогда число подвижных звеньев , число пар пятого класса, число пар четвертого класса  Условием существования структурной группы с низшими кинематическими парами:

 

                                  (4)

Подставим выявленные значения коэффициентов в выражение (4) получим:

.

Следовательно, группа звеньев 2 – 3 является структурной группой Ассура 2 класса (т.к. ) 2 порядка (т.к. два поводка) 2 вида (т. к ПВП).

Вторая Группа звеньев 0 – 1 рис. 4.

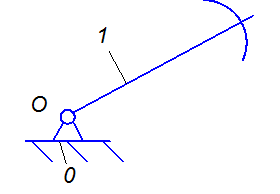
Рисунок 4 – первичный механизм

Данная группа состоит из подвижного звена кулисы 1, стойки 0 и одной кинематической пары 0 – 1 – вращательная пятого класса, тогда .

Подставим выявленные значения коэффициентов в выражение (4) получим:

.

Следовательно, группа звеньев 0 – 1 не является структурной группой Ассура, а представляет собой первичный механизм, подвижность которого равна 1.

Формула состава структуры механизма:

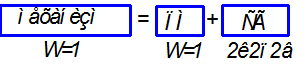
Класс механизма определяется классом наиболее сложной структурной группы. Рассмотренный механизм является механизмом второго класса.

 Задание 3.

Для того чтобы построить кинематическую схему механизма необходимо выбрать масштабный коэффициент длин . Рассчитывается по следующей формуле:

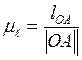,                                                      (5)

где      - масштабный коэффициент ;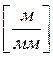

           - действительная длина кривошипа, измеряемая в метрах;

           - отрезок, взятый в миллиметрах изображающий действительную длину кривошипа  в принятом масштабный коэффициент длин.

.

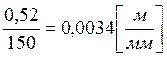Переводим все заданные геометрические параметры механизма (длины звеньев) имеющие размерность длин (м) в масштаб коэффициент.

Для этого действительные длины звеньев в метрах делим на полученный масштабный коэффициент длин и получаем длину звена, которая будет на чертеже в миллиметрах.

.

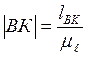,                                                     (6)

 Получаем следующие значения:

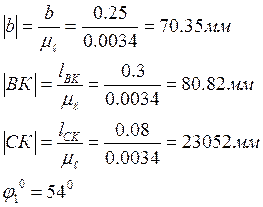
Теперь, когда все размеры звеньев механизма переведены в масштабный коэффициент можно приступать к построению кинематической схемы.

 На плоскости формата произвольно ставим точку О. В направлении против часовой стрелки

угол и в заданном направлении от точки О отмеряем отрезок ОА длиной равный длине кулисы 1.

В точке А кулиса соединена с камнем, вычерчиваем 2 элемент структуры. Через камень проводим вертикальную прямую. От точки О откладываем отрезок длиной равный значению параметра . На конце отрезка, обозначим точкой D, будут располагаться один из элементов стойки 0.

От точки В вниз по вертикали откладываем отрезок длиной равный