Кинематический анализ плоских рычажных механизмов

звеньев) имеющие размерность длин (м) в масштаб коэффициент.

Для этого действительные длины звеньев в метрах делим на полученный масштабный коэффициент длин и получаем длину звена, которая будет на чертеже в миллиметрах.

.

,                                                     

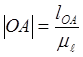 Получаем следующие значения:

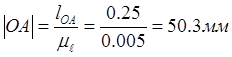
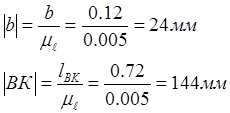
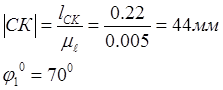
Теперь, когда все размеры звеньев механизма переведены в масштабный коэффициент можно приступать к построению кинематической схемы.

Крайними положениями являются положения выходного звена, в которых кулиса 1 меняет свой вид движения, такими является нулевое положение и второе.

Ход механизма (Н), рассчитывается между начальным и конечным положениями выходного звена, в данном механизме он равен длине кулисы 3.

Н=166мм

Коэффициент неравномерности средней скорости – это коэффициент, характеризующий отношение времени холостого хода к времени рабочего хода :

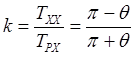
где  - угол  между положениями шатуна в крайних положениях механизма.

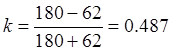
Угол давления - острый угол между вектором активной силы Р_а действующий со стороны предшествующего звена и вектором скорости точки ее приложения этой силы.

 В нулевом положении механизма, угол давления принимает максимальное значение и равен .

В седьмом положении механизма, угол давления принимает минимальное значение и  равен .

Задание  2.

Для построения первой диаграммы пути, задаемся масштабным коэффициентом оси пути и оси времени :

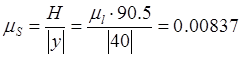
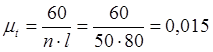
где     n –  число оборотов кривошипа, мин^-1

 - произвольный отрезок, мм.

Одно из крайних положений выходного звена примем за начальное положение. Измерив отрезок , найдем перемещение выходного звена относительно первого положения кривошипа. Отложив найденный отрезок, получим точку диаграммы пути соответствующую первому положению кривошипа. Проведя аналогичные действия, найдем точки диаграммы для всех остальных положений кривошипа. Отрезок  рассчитываем по следующему выражению:

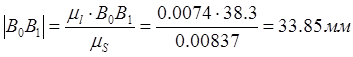
Для остальных отрезков производим аналогичные действия:

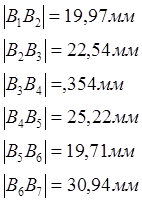
Соединив точки плавной кривой, получим диаграмму пути являющейся функцией от времени .

Для построения второй диаграммы аналога скорости, используем графическое дифференцирование кривой пути. Масштабный коэффициент оси времени приравниваем к масштабному коэффициенту оси диаграммы пути. На продолжении оси времени откладываем отрезок , получим точку  - полюс дифференцирования .

Масштабный коэффициент оси аналога скорости, :

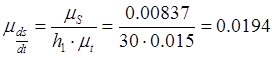
Через точки кривой пути проводим касательные. Через полюс точку  проводим лучи параллельно касательным. соединяя точки пересечения оси аналога скоростей с лучами, получаем диаграмму аналога скоростей являющейся функцией от времени .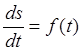

Для построения третьей диаграммы аналога ускорений, используем графическое дифференцирование диаграммы аналога скорости. Масштабный коэффициент оси времени приравниваем к масштабному коэффициенту предшествующих диаграмм . На продолжении оси времени откладываем отрезок , получим точку  - полюс дифференцирования

Масштабный коэффициент оси аналога ускорения, :

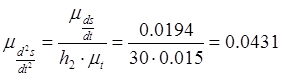
Через точки кривой аналога скорости проводим касательные. Через полюс точку  проводим лучи параллельно касательным. соединяя точки пересечения оси аналога ускорения с лучами, получаем диаграмму аналога ускорений являющейся функцией от времени .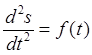

Задание 3.

Проанализируем схему тангенсального механизма: точка О является неподвижной, следовательно, модуль скорости этой точки равен нулю:

.

Вектор скорости точки А представляет собой геометрическую сумму вектора скорости точки О и скорости относительно вращательного