Структурный, кинематический и силовой анализы плоского рычажного механизма, состоящего из пяти подвижных звеньев, двух шарнирно неподвижных опор и направляющей

Первая структурная группа механизма образована звеньями 4 и 5, входящими в две вращательные пары 4–3 и 4–5 и одну поступательную пару 0–5, и является группой II класса (так как состоит из двух подвижных звеньев), второго вида – имеет структурную формулу ВВП (так как две пары вращательные и одна поступательная), второго порядка (так как имеет два поводка). Подвижность структурной группы механизма равна нулю .

Рисунок 4 – Вторая структурная группа механизма (2 - 3)

Вторая структурная группа механизма образована звеньями 2 и 3, входящими в три вращательные пары 1–2, 2–3 и 3 - 0, и является группой II класса, первого вида и второго порядка. Подвижность структурной группы механизма равна нулю .

2.4 Первичный механизм

Рисунок 5 – Первичный механизм

Первичный механизм является механизмом первого класса и его подвижность равна:

.

Структурная формула механизма

 

=                        +                          +

Таким образом, данный плоский рычажный механизм обладает одной степенью свободы и является механизмом II класса. Класс механизма определяется наивысшим классом структурной группы механизма, входящей в данный механизм.

3 Структурный синтез плоского рычажного механизма

3.1 Кинематическая схема механизма

Построим кинематическую схему механизма, для этого вычислим масштабный коэффициент длины :

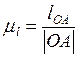,                                                     где  – действительная длина кривошипа в метрах;

 – размер кривошипа в миллиметрах принимаемый на чертеже и характеризующий длину кривошипа на кинематической схеме.

.

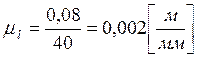Остальные размеры звеньев вычислим по формуле:

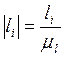,                                                        где  – номер звена, для которого вычисляется длина на кинематической схеме.

,

,

,

.

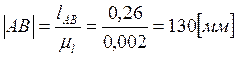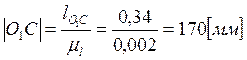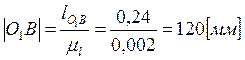
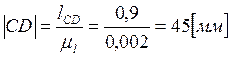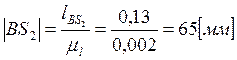
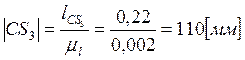
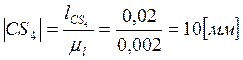
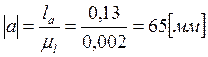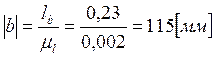
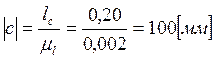
На плоскости выбираем произвольную точку О. Из точки О радиусом  проводим окружность, для построения 12-ти положений механизма окружность разбивают на двенадцать частей. Из точки О проводим горизонтальный отрезок диной , затем проводим прямую DE под углом 90º к отрезку с, которая будет являться направляющей ползуна 5. В противоположную сторону отрезку с откладываем отрезок длинной  ,  затем перпендикулярно к нему – отрезок  длинной, таким образом получаем точку О1 в которой будет расположена вторая шарнирно неподвижная опора. (первая расположена в точке О). Проводим отрезок ОА, из точки А, после чего проводим дугу окружности радиусом  до пересечения с окружностью, проводим отрезок АВ. На продолжении О1В откладываем отрезок длиной , получаем точку С. Из точки С проводим дугу окружности радиусом  до пересечения с прямой DE, проводим отрезок CD. (Кинематическая схема представлена в приложении А)

4 Кинематический анализ рычажного механизма

 

4.1 Положения механизма

 Аналогично построению кинематической схемы построим 12-ть положений механизма. (План положений представлен на листе 1 графической части)

Сначала найдём крайние положение механизма. Под крайними положениями подразумеваются такие положения выходных звеньев, в которых оси кривошипа 1 и шатуна 2 совпадают. Положения точки В  в крайних положениях механизма найдем проведя из точки О дуги радиусами:

 ,

,

до пересечения с окружностью О1В . Положения точки  А соответствующие крайним положениям точки В найдем проведя, из точки О окружность радиусом .За нулевое (начальное) положение выберем нижнее крайнее положение. Проводим нумерацию положений звеньев механизма.

4.2 Линейные и угловые скорости точек механизма

Найдем линейные скорости точек звеньев для 12-ти положений механизма:

Рассмотрим ведущее звено механизма (Рисунок 6 ):

Рисунок 6 – Схема ведущего звена

Угловую скорость первого звена найдём по формуле:

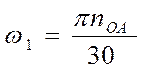,                                          где  – частота вращения первого звена.

.

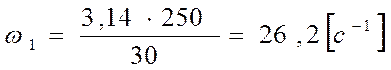При вращательном движении первого звена скорость точки А этого звена направлена перпендикулярно её радиусу вращения по направлению и равна:

 

,                                                

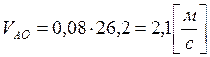
Согласно определению плоскопараллельного движения, скорость любой точки этого тела будет определяться через скорость полюса следующим образом:

,                              

, где  – скорость точки А;

 – скорость точки О, взятой за полюс;

 – скорость вращения точки А вокруг точки О.

Зададим масштабный коэффициент скоростей :

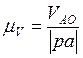,                                                     где  – значение скорости вращения точки А вокруг точки О;

 – длина отрезка  на плане скоростей, представляющая скорость  на плане скоростей.

Возьмем масштаб:

.

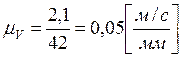Выбираем в качестве полюса плана скоростей произвольную точку p  проводим в выбранном масштабе вектор .

Для нахождения скорости точки В рассмотрим плоское движение второго звена, взяв за полюс точку А. Тогда будем иметь:

,                                       где  – неизвестная скорость точки В;

 – известная по величине и направлению скорость точки А;

 – скорость точки В при её вращении вокруг точки А, направленная перпендикулярно АВ .

Рассматривая вращательное движение третьего звена и взяв за полюс