Оценка показателей свойств надежности двигателя автомобиля

2.1 Оценка показателей свойств надежности

2.1.1 Оценка средней наработки до отказа

Вариационный ряд наработки элемента до 1 замены, тыс. км.:

Упорядоченный вариационный ряд, и посчитанное количество чисел:

N=30 – объем выборки

2.1.2 Точечная оценка

Выборочная средняя (тыс.км.):

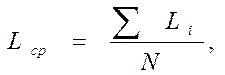(1)

где Li – i-й член вариационного ряда, (тыс. км.);

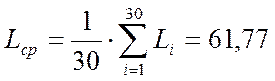               (2)

Дисперсия (тыс. км.)²:

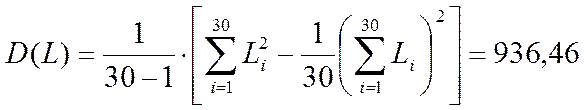         (3)               

Среднеквадратичное отклонение (тыс. км.):

        (4)

Коэффициент вариации:

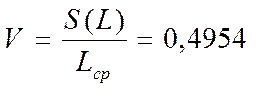      (5)

b – параметр формы закона Вейбула-Гнеденко, берем b=2,1481

2.1.3 Интервальная оценка

Предельная относительная ошибка:

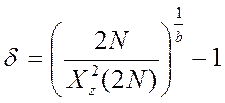           (6)

где Х²_z – критерий Пирсона (при =0,9, 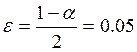), где - вероятность, - уровень значимости,

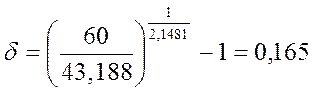        (7)

Верхние и нижние границы доверительного интервала, (тыс. км.):

L_н = L_cp*(1-) = 51,551             (9)

L_в = L_cp*(1+) = 71,983          (10)

[] (тыс. км.) – отказ произойдет в этом интервале.

2.1.4 Оценка параметра масштаба закона Вейбула-Гнеденко

Параметр масштаба закона Вейбула-Гнеденко (тыс. км.):

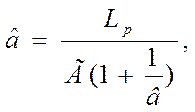            (11)

где Г(1+1/в) – гамма-функция,

Г(1+1/в)=0,8857

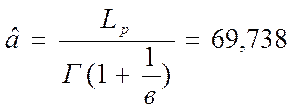
Граничные значения интервальной оценки (тыс. км.):

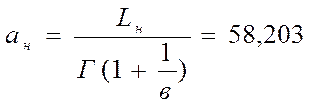         (12)

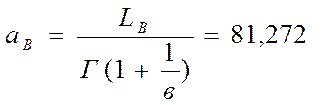       (13)

2.1.5 Проверка нулевой гипотезы

Х²_рас  Х²_табл  () – условие соблюдения нулевой гипотезы,

Где Х²_рас – значение критерия согласия Пирсона, вычисленное по экспериментальным данным;

Х²_табл – критическая точка критерия

Где - уровень значимости, к – число степеней свободы,

 = 0,1

где S – количество частичных интервалов выборки,

r – количество параметров предполагаемого распределения,

r=2.

Количество интервалов Sпо правилу Штюргеса:

S=1+3.32*lgN;

S=6;

k=S-1-r,

k=3;

X²_табл. = 6,251

Протяженность интервала (тыс. км.):

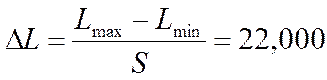        (14)

где L_max – наибольший элемент, L_min – наименьший элемент.

2.1.6 Расчет эмпирических частот

L₁₊₁=L_min+L; L₂₊₁=L_min+2L,              

Таблица 1 – Расчет эмпирических частот

2.1.7 Расчет теоретических частот

         (15)

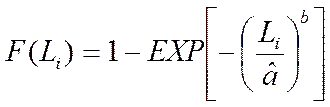,          (16)

где F(L) – функция распределения отказов;

   (17)

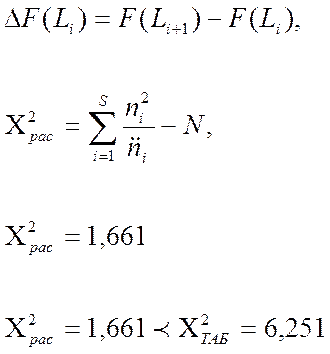
 (18)

(19)

- Нулевая гипотеза выполняется

Таблица 2 – Расчет Х²_рас

2.1.8 Оценка плотности распределения отказов (отказ/тыс.км)

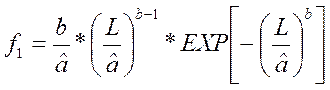          (20)

Таблица 3 – Плотность распределения наработок до первого отказа элемента

График плотности распределения отказов двигателя автомобиля

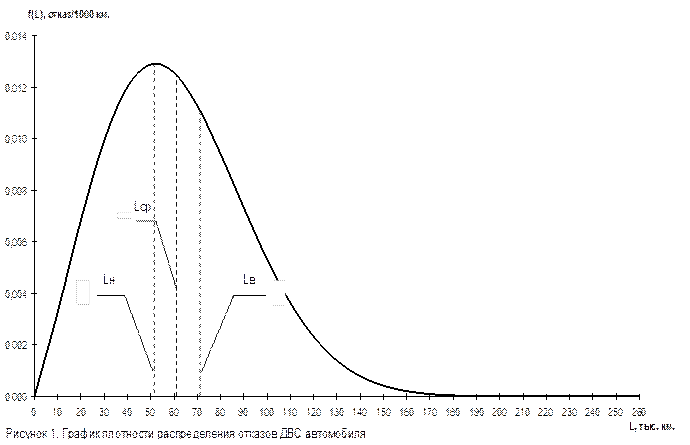
График показывает плотность вероятности того, что наработка элемента АТС до отказа окажется меньше L.

2.1.9 Оценка количественных характеристик безотказности и долговечности

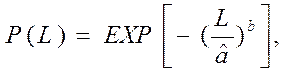              (21)

где P(L) – вероятность безотказной работы.

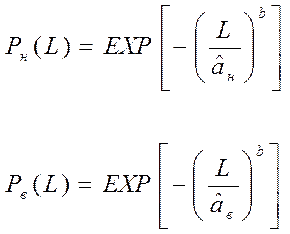
- нижняя доверительная граница

- верхняя доверительная граница

Таблица 4 – Точечная оценка вероятности безотказной работы элемента до первого отказа (Нижние и верхние доверительные границы)