Другие предметы \ Научно-исследовательская работа студента

Оценка показателей свойств надежности двигателя автомобиля, страница 2

L, тыс. км.

Pв(L)

P(L)

Pн(L)

0

1,0000

1,0000

1,0000

10

0,9890

0,9847

0,9775

20

0,9520

0,9339

0,9041

30

0,8891

0,8493

0,7860

40

0,8040

0,7386

0,6397

50

0,7031

0,6130

0,4860

60

0,5939

0,4848

0,3439

70

0,4840

0,3649

0,2262

80

0,3803

0,2611

0,1380

90

0,2879

0,1774

0,0780

100

0,2099

0,1143

0,0408

110

0,1472

0,0698

0,0197

120

0,0993

0,0404

0,0088

130

0,0644

0,0221

0,0036

140

0,0401

0,0115

0,0014

150

0,0240

0,0056

0,0005

160

0,0138

0,0026

0,0002

170

0,0076

0,0011

0,0000

180

0,0040

0,0005

0,0000

190

0,0020

0,0002

0,0000

200

0,0010

0,0001

0,0000

210

0,0005

0,0000

0,0000

220

0,0002

0,0000

0,0000

230

0,0001

0,0000

0,0000

240

0,0000

0,0000

0,0000

График вероятности безотказной работы двигателя автомобиля

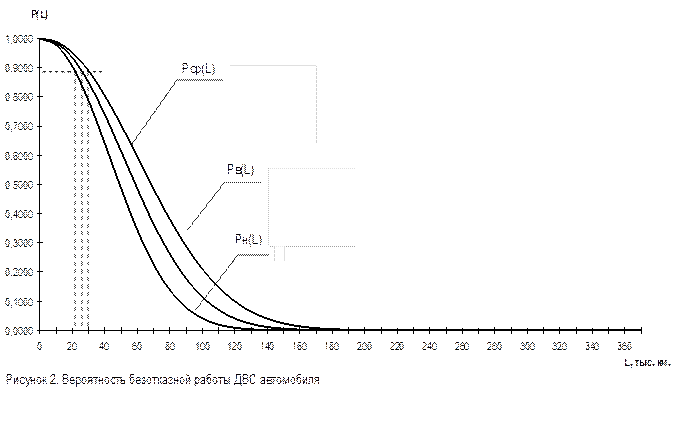
По графику можно оценить гамма-процентную наработку до первого отказа Для этого параллельно оси абсцисс проводят прямую линию через точку P(L)=j%/100. Пусть j=90%. Тогда P(L)=0,9. Абсциссы точек пересечения этой прямой с кривыми P(L)-ср., ниж., вер., дают точечную и интервальную оценку гамма - процентной наработки до первого отказа.

2.1.10 Оценка гамма - процентной наработки до отказа (тыс. км):

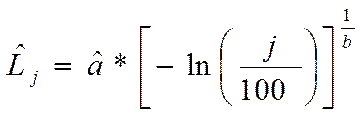     (22)

где j – вероятность, с которой не возникает отказ элемента АТС при наработке

P(L)=90% / 100 = 0.9

j=90%

L90%B = 28,508 тыс. км

L90%CP = 24,462 тыс. км

L90% H = 20,416 тыс. км

2.1.11 Точечная оценка интенсивности отказов элемента

Интенсивность отказов (отказ/тыс. км)

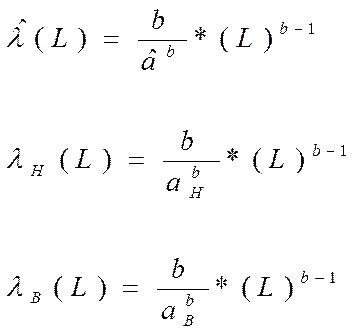 (22)

 (23)

(24)

Таблица 7 – Точечная оценка интенсивности отказов элемента (Верхние и нижние доверительные границы)

Скачать файл