Другие предметы \ Научно-исследовательская работа студента

Оценка показателей свойств надежности двигателя автомобиля, страница 3

L, тыс. км.	λв(L)	λср(L)	λн(L)	L, тыс. км.	λв(L)	λср(L)	λн(L)
0	0,0000	0,0000	0,0000	190	0,0701	0,0973	0,1435
10	0,0024	0,0033	0,0049	200	0,0743	0,1032	0,1522
20	0,0053	0,0073	0,0108	210	0,0786	0,1092	0,1610
30	0,0084	0,0117	0,0172	220	0,0829	0,1152	0,1699
40	0,0117	0,0163	0,0240	230	0,0873	0,1212	0,1787
50	0,0151	0,0210	0,0310	240	0,0916	0,1273	0,1877
60	0,0187	0,0259	0,0382	250	0,0960	0,1334	0,1967
70	0,0223	0,0309	0,0456	260	0,1004	0,1395	0,2058
80	0,0260	0,0361	0,0532	270	0,1049	0,1457	0,2149
90	0,0297	0,0413	0,0609	280	0,1094	0,1519	0,2240
100	0,0335	0,0466	0,0687	290	0,1139	0,1582	0,2332
110	0,0374	0,0520	0,0766	300	0,1184	0,1645	0,2425
120	0,0413	0,0574	0,0847	310	0,1229	0,1708	0,2518
130	0,0453	0,0630	0,0928	320	0,1275	0,1771	0,2611
140	0,0493	0,0686	0,1011	330	0,1321	0,1835	0,2705
150	0,0534	0,0742	0,1094	340	0,1367	0,1899	0,2800
160	0,0575	0,0799	0,1178	350	0,1413	0,1963	0,2894
L, тыс. км.	λв(L)	λср(L)	λн(L)	L, тыс. км.	λв(L)	λср(L)	λн(L)
170	0,0617	0,0857	0,1263	360	0,1459	0,2027	0,2990
180	0,0659	0,0915	0,1349	370	0,1506	0,2092	0,3085

График интенсивности первых отказов двигателя

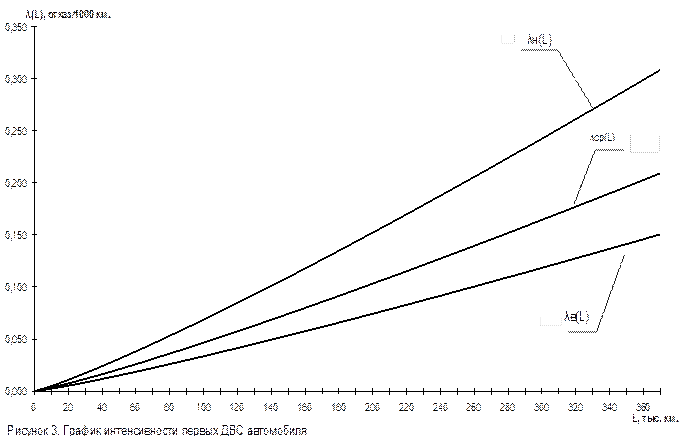
Вывод: По построенным графикам можно определить зависимость наработок до первого отказа, по которым рассчитываются: вероятность безотказной работы, интенсивности отказов, плотность распределения отказов – которые образуют точечные интервальные наработки до первого отказа двигателя автомобиля .

По графику интенсивности первых отказов элементов , тыс. км.^-1, можно определить, что плотность вероятности возникновения отказа двигателя автомобиля определяется данным моментом времени и до этого момента отказ не возникает.

По графику плотности распределения отказов f(L), тыс. км., можно определить, что плотность вероятности того, что наработка двигателя автомобиля до отказа окажется меньше L тыс. км.

По графику вероятности безотказной работы P(L), можно определить, что наработка, в течении которой отказ двигателя автомобиля не возникнет с вероятностью j%, при Р=0,9.

3.1 Прогнозирование потребностей количества запасных частей по наработке

Q(L)=N*F(L), где N – количество элементов,

Q(L) – количество запасных частей,

F(L) – вероятность отказа элемента при данной наработке.

F(L)=1-P(L).

Таблица 8 – Расчет потребностей запасных частей

L, тыс. км.	50	100	130	160	250
P(L)	0,6130	0,1143	0,0221	0,0026	0,0000
F(L)	0,3870	0,8857	0,9779	0,9974	1,0000
Qз.ч., шт.	12	27	29	30	30

Вывод: Судя по данным, - с увеличением пробега, увеличивается количество запасных частей.

1 2 3

Скачать файл