Упрощённая методика расчёта дисковых и барабанно-колодочных тормозов: Методические указания, страница 8

Здесь:  – коэффициент трения между рабочими поверхностями тормозного барабана и фрикционными накладками колодок;  – радиус рабочей поверхности тормозного барабана, м;  – расстояние от оси колеса до линии действия разжимных сил колодок (или до оси колёсных цилиндров), м;  – расстояние от оси колеса до линии, соединяющей оси опор передней и задней колодок, м;  – разность между радиусом  тормозного барабана и половиной расстояния между опорами передней и задней колодок (см. рис. 6а), м.

Для автомобиля категории М1 класса "Волга"  /3/.

Из (3.9) и (3.10), имеем

.

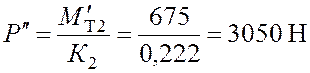Реализовать необходимую разжимную силу  колёсного цилиндра заднего тормозного механизма можно за счёт подбора диаметра этого цилиндра  и давления  тормозной жидкости в гидромагистрали. Для этой цели воспользуемся с некоторыми изменениями уравнением (3.7)

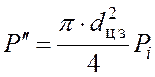.                                        (4.11)

Здесь:  – диаметр колёсного цилиндра тормозного механизма задних колёс.

Принятый нами  мм, тогда из (3.11) получаем

.

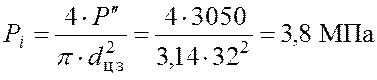Таким образом, для реализации на задних колёсах требуемого тормозного момента необходимо иметь в гидросистеме давление , а на передних колёсах – . Давление же тормозной жидкости в гидросистеме, создаваемое водителем (4.8) при усилии на педали , составляет . Этого давления не достаточно даже для тормозных механизмов задних колёс, а тем более – для передних.

Есть несколько возможных вариантов решения этой проблеммы:

а) установить в гидросистеме вакуумный усилитель, обеспечивающий давление , с коэффициентом усиления 1,34 = 3,8/2,84 при увеличении диаметра тормозного цилиндра переднего колеса до величины (4.7)

;

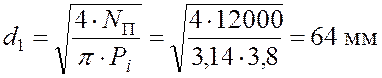б) не изменяя размеров тормозных цилиндров передних и задних колёс, применить раздельные приводы к передним и задним осям с коэффициентами усиления соответственно  и .

С точки зрения безопасности движения второй вариант предпочтительней, так как при отказе одного контура гидропривода, второй контур сможет обеспечить затормаживание автомобиля. Однако такая тормозная система окажется значительно сложнее одноконтурной. В каждом конкретном случае конструктор должен выбирать ту или иную систему с учётом её плюсов и минусов.

4.4. Определение хода тормозной педали автомобиля с передними дисковыми и задними барабанно-колодочными тормозными механизмами

Используя уравнение (1.14) из первого раздела (дисковые тормоза) и уравнение (3.17) из третьего раздела (барабанно-колодочные тормоза), получим новое уравнение

.                                        (4.12)

Здесь:  – диаметр главного тормозного цилиндра, м;  – ход поршня главного гидроцилиндра, м;  – диаметры колёсных цилиндров соответственно передних и задних колёс;  – зазор между поршнем и колодкой (ход поршня тормозного механизма переднего колеса ());  – суммарные перемещения поршней каждого колёсного цилиндра тормозных механизмов задних колёс. Цифра 4 в правой части уравнения указывает на то, что в дисковом тормозном механизме передних колёс на каждом колесе установлены два поршня и, следовательно в сумме на переднюю ось их четыре. В барабанно-колодочных механизмах двух задних колёс установлено по одному цилиндру, т. е. всего два.

Из (4.12) получаем окончательно

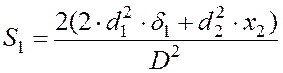.                                          (4.13)

Полный ход педали будет

,                                          (4.14)

где  – зазор между штоком и поршнем главного тормозного цилиндра в расторможенном состоянии ( мм);  – передаточное число педали

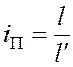.                                          (4.15)

Здесь:  – соответственно большее и меньшее плечи педали.

Для легковых автомобилей , для грузовых .

Из (4.14) с учётом (4.13) получим

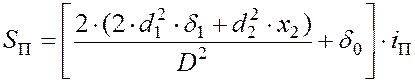.                                          (4.16)

Максимальный ход педали тормоза не должен превышать для легковых автомобилей  мм, для грузовых –  мм.