Лабораторная работа №4
Задание
Найти вероятность безотказной работы зубчатой передачи, если известно: межосевое расстояние aw=130 мм, число зубьев шестерни n=8, рабочая ширина зубчатого венца bw=21 мм, модуль передачи m=1,5 мм, передаточное число u=2,4. Зубчатые колеса после улучшения имеют твердость HB=300. При работе в номинальном режиме на шестерне возникает крутящий момент M1H=160 Н×м при внешней нагрузке моментом М=220 Н×м.
|
Исходные данные |
Косозубые передачи |
|
d1, мм |
35 |
|
ZH |
2,34 |
|
vA |
1,3 |
|
KHb |
1,02 |
|
aHa |
0,45 |
|
bHa |
1 |
|
c |
0,9 |
|
YF |
3,22 |
|
Yb |
0,819 |
|
KHL |
2,25 |
|
vsF |
1,1 |
|
ea |
1,4 |
|
KFV |
1,02 |
|
K0Fb |
1,11 |
|
KFW |
0,816 |
|
Da |
0,5 |
Решение
Вероятность безотказной работы зубчатой передачи определяется как произведение вероятностей безотказной работы по отдельным критериям. Для широкого круга зубчатых передач, у которых наиболее опасны усталостные разрушения, вероятность безотказной работы равна:
P = PH ×PF,
P = 1 ×0,56=0,56
где PH – вероятность безотказной работы по критерию сопротивления усталости при контакте;
PF – вероятность безотказной работы по критерию сопротивления усталости при изгибе.
1. Расчет на сопротивление контактной усталости.
Вероятность безотказной работы по критерию сопротивления контактной усталости PH определяется как вероятность того, что контактное напряжение (расчетный параметр) sН не превышает предела контактной выносливости (предельного значения расчетного параметра) sH lim, т.е. РН = Вер (sН<sH lim ).
Контактное напряжение sН, МПа, действующее в полюсе зацепления:
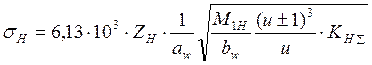 , где
ZH–
коэффициент, учитывающий форму сопряженных поверхностей;
, где
ZH–
коэффициент, учитывающий форму сопряженных поверхностей;
aw– межосевое расстояние, мм;
bw– рабочая ширина венца, мм;
u – передаточное число;
М1H – крутящий момент на шестерне при работе в номинальном режиме (сокращенно номинальный момент), Н´м;
КНå - коэффициент нагрузки.
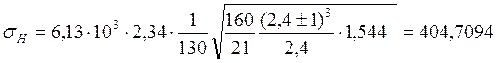
Напряжение sН рассматривает как функцию случайной величины КНå , равной произведению четырех случайных величин:
![]()
![]()
где КА – коэффициент внешней нагрузки;
КНb - коэффициент, учитывающий распределение нагрузки по ширине венца;
КHV – коэффициент, учитывающий динамическую нагрузку, возникающую в зацеплении;
КНa - коэффициент, учитывающий распределение нагрузки между зубьями.
Номинальный момент М1H и другие параметры в формуле для sН считаем детерминированными величинами. Случайный характер внешней нагрузки учитываем коэффициентом внешней нагрузки КА.
Коэффициент вариации нагрузки определяется как коэффициент вариации произведения независимых случайных множителей:
![]() ,
,
![]()
где vA, vHb, vHV, vHa - коэффициенты вариации соответственно КА, КНb, КHV, КНa.
В настоящем расчете коэффициент КА внешней нагрузки выделен в самостоятельный. Это уменьшает вероятность недоучета внешней динамики и рассеяния внешней нагрузки по сравнению с формой расчета, по которой они учитываются при назначении внешней нагрузки. Внешние дополнительные нагрузки в машинах оцениваются специалистами по отдельным отраслям машиностроения на основе обобщения опыта эксплуатации и решения динамических задач для систем с двигателями и исполнительными механизмами.
В
расчетах, где внешняя динамика учтена в задаваемой внешней нагрузке (моменте)
М, среднее значение ![]() и коэффициент вариации vM
коэффициента внешней нагрузки соответственно равны:
и коэффициент вариации vM
коэффициента внешней нагрузки соответственно равны:
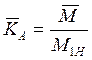 , vA
= vМ.
, vA
= vМ.
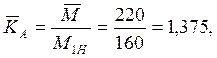
Среднее
значение коэффициента ![]() определяется по формуле для КНb,,
где вместо gD подставляют
среднее значение
определяется по формуле для КНb,,
где вместо gD подставляют
среднее значение ![]() . Здесь составляющая,
пропорциональная упругому перекосу зубьев, может рассматриваться как
детерминированная, а пропорциональная погрешностям изготовления как случайная.
В среднем можно принять детерминированную составляющую равной двум третям от
среднего относительного приращения, этому же значению будет равно поле
рассеяния дополнительной относительной случайной нагрузки. Полагая, что поле
рассеяния перекрывается шестью средними квадратическими отклонениями, получаем
выражение для коэффициента вариации:
. Здесь составляющая,
пропорциональная упругому перекосу зубьев, может рассматриваться как
детерминированная, а пропорциональная погрешностям изготовления как случайная.
В среднем можно принять детерминированную составляющую равной двум третям от
среднего относительного приращения, этому же значению будет равно поле
рассеяния дополнительной относительной случайной нагрузки. Полагая, что поле
рассеяния перекрывается шестью средними квадратическими отклонениями, получаем
выражение для коэффициента вариации:
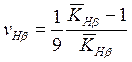 ,
,
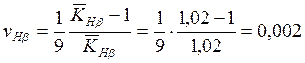
Случайный характер коэффициента КHV учитывающего динамическую нагрузку, определяется случайностью составляющих его величин. Коэффициент рассчитывается по формуле:
КHV = 1+сХ,
КHV = 1+0,9*0,177=1,159
где
![]() ,
,
![]()
с – коэффициент, пропорциональный окружной скорости, приведенной массе и обратно пропорциональный передаваемой удельной нагрузке;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.